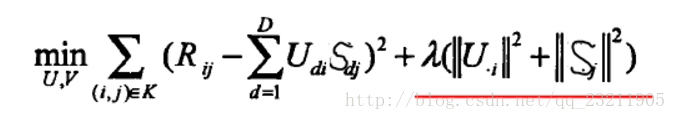基於矩陣分解的推薦演算法(java程式碼實現)
阿新 • • 發佈:2019-01-01
目前推薦系統中用的最多的就是矩陣分解方法,在Netflix Prize推薦系統大賽中取得突出效果。以使用者-專案評分矩陣為例,矩陣分解就是預測出評分矩陣中的缺失值,然後根據預測值以某種方式向用戶推薦。常見的矩陣分解方法有基本矩陣分解(basic MF),正則化矩陣分解)(Regularized MF),基於概率的矩陣分解(PMF)等。今天以“使用者-專案評分矩陣R(N×M)”說明三種分解方式的原理以及應用。
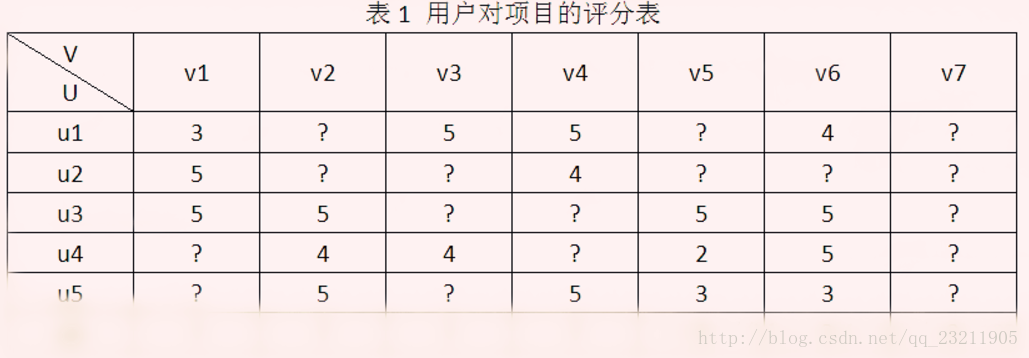
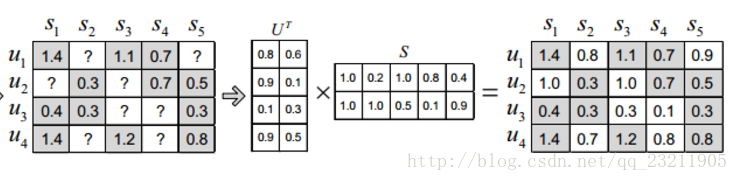
使用者-專案評分矩陣
Basic MF:
Basic MF是最基礎的分解方式,將評分矩陣R分解為使用者矩陣U和專案矩陣S, 通過不斷的迭代訓練使得U和S的乘積越來越接近真實矩陣,矩陣分解過程如圖:
矩陣分解過程
預測值接近真實值就是使其差最小,這是我們的目標函式,然後採用梯度下降的方式迭代計算U和S,它們收斂時就是分解出來的矩陣。我們用損失函式來表示誤差(等價於目標函式):
損失函式 公式1
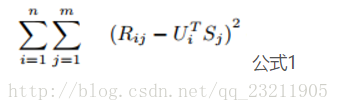
公式1中R_ij是評分矩陣中已打分的值,U_i和S_j相當於未知變數。為求得公式1的最小值,相當於求關於U和S二元函式的最小值(極小值或許更貼切)。通常採用梯度下降的方法:
梯度下降
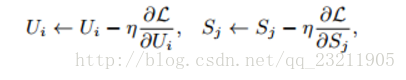
學習速率是學習速率,表示迭代的步長。其值為1.5時,通常以震盪形式接近極值點;若<1迭代單調趨向極值點;若>2圍繞極值逐漸發散,不會收斂到極值點。具體取什麼值要根據實驗經驗。
Regularized MF
正則化矩陣分解是Basic MF的優化,解決MF造成的過擬合問題。其不是直接最小化損失函式,而是在損失函式基礎上增加規範化因子,將整體作為損失函式。
紅線表示正則化因子,在求解U和S時,仍然採用梯度下降法,此時迭代公式變為:(圖片擷取自相關論文,S和V等價)
梯度下降
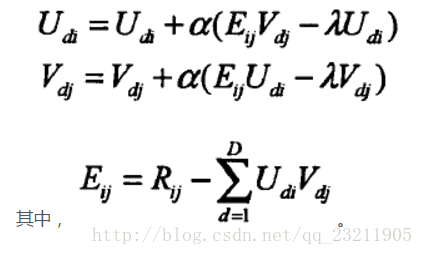
梯度下降結束條件:f(x)的真實值和預測值小於自己設定的閾值(很小的值,之前一直理解為是變數U和V的迭代值差小於閾值就行)
Java程式碼實現矩陣分解
public class Test {
private static int N=5;//使用者的數目
private static