資料結構(一)-----二叉樹
一、二叉樹簡介
1、二叉樹簡介
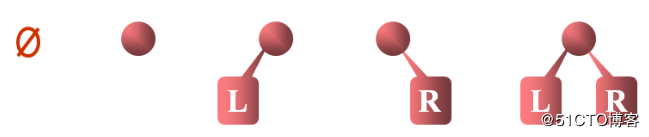
二叉樹是由n(n>=0)個結點組成的有序集合,集合或者為空,或者是由一個根節點加上兩棵分別稱為左子樹和右子樹的、互不相交的二叉樹組成。
性質一:對於任何一棵二叉樹T,若葉子節點數為n0,度數為2的節點數為n2,則n0=n2+1
假設二叉樹節點總數為n,度數為1的節點個數為n1,則n=n0+n1+n2成立,除根節點外,其它節點通過一條樹枝且僅通過一條樹枝與其父節點相連,而二叉樹中樹枝總數為n1+2*n2,加上根節點後可得總結點數為n=n1+2*n2+1,所以n0=n2+1
3、滿二叉樹
如果二叉樹中所有分支結點的度數都為2,並且最後一層的葉子節點(葉子節點是指沒有兒子節點)都存在,則二叉樹為滿二叉樹。

4、完全二叉樹
如果一棵具有n個結點的高度為k的二叉樹,扣除最後一層後的樹是滿二叉樹且層次最大的那層所有葉子節點均向左靠齊,則二叉樹為完全二叉樹。
完全二叉樹的特性:
A、同樣結點數的二叉樹,完全二叉樹的高度最小
B、完全二叉樹的葉子結點僅出現在最下邊兩層,並且最底層的葉子結點一定出現在左邊,倒數第二層的葉子結點一定出現在右邊。
C、完全二叉樹中度為1的結點只有左孩子。
D。完全二叉樹中節點度數為1的節點數最多為1

題目一:若有一棵完全二叉樹有1000個節點,請問葉子節點數?度數為2的節點數?度數為1節點數?
首先有n=n0+n1+n2,且n0=n2+1; n=n1+2*n2+1=1000,因為為完全二叉樹,所以可以推出度數為1的節點數最多為1,欽此我們可以推出只有當n1=1,n=n1+2*n2+1=1000才合理,故得n0=500,n2=499,n1=1
題目二:一棵樹,度數為1節點數有4,度數為2節點數有3,度數為3節點數有2,度數為4節點數有1,求葉子節點數
可以根據1*4+2*3+3*2+4*1+1=4+3+2+1+n0->n0=10
5、二叉樹的特性 (根節點為第一層)
A、在二叉樹的第i層上最多有2^(i-1)個結點(i>=1)。
B、高度為k的二叉樹,最多有2^k-1個結點(k>=0)。
C、對任何一棵二叉樹,如果其葉結點有n個,度為2的非葉子結點有m個,則
n = m + 1。
D、具有n個結點的完全二叉樹的高度為logn + 1
E、對於有n個結點的完全二叉樹,按層次對結點進行編號(從上到下,從左到右),對於任意編號為i的結點:

