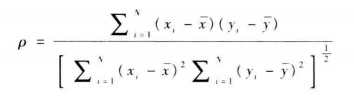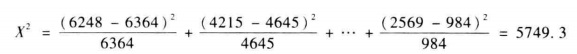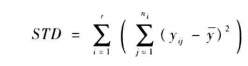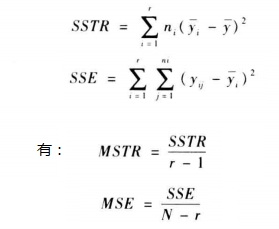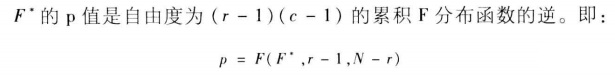信用風險評估之 預測力指標(篩選特徵)
在建模時,被用來預測的變數(即feature)相互間不能有很強的相關性,最好完全不存在相關性。
評判變數間的預測力指標有皮爾森相關係數,斯皮爾曼相關係數,皮爾森卡方統計量,概率比,資訊值等。
1.皮爾森相關係數pearson
連續變數x,y(兩列feature), 皮爾森相關係數ρ:
取值區間[-1,1]。
0表示無相關性即相互獨立,越接近於0,相關性越小;
-1為負的強相關性;
+1為正的強相關性。
去均值化的ρ即為餘弦夾角公式:
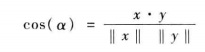
小結:
1》皮爾森相關係數會受資料錯誤或極端值的影響而不穩定。
2》皮爾森相關係數計算的是每個觀測值與均值間的差值,適合連續變數間的相關性計算,就不適合
3》越接近0,相關性越小。
2.斯皮爾曼相關係數spearman
斯皮爾曼相關係數的計算採用取值的等級,而不是取值本身。當取值按升序排列時,取值的等級就是該取值的順序。如12,5,8的等級為3,1,2。計算公式類似皮爾森相關係數:
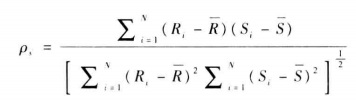
R,S是兩個變數的取值對應的等級。
小結:
1》斯皮爾曼相關係數適用於順序變數間的相關性計算。
2》斯皮爾曼相關係數對於資料錯誤和極端值不敏感。
3》越接近於0,相關性越小。
3.皮爾森卡方統計量
皮爾森卡方統計量用X²表示,衡量兩個名義變數間的相關性。
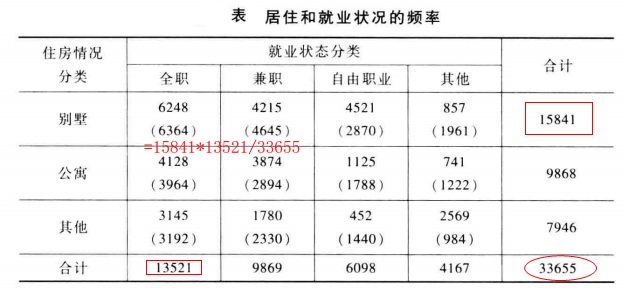
下面以一個例子來說明卡方統計量,如下為住房與就業的人數統計表。
第i行第j列的預期頻數為:
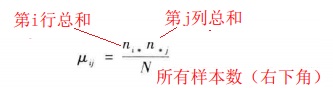
也即表格中小括號中的計算資料。
卡方統計量的定義如下:
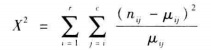
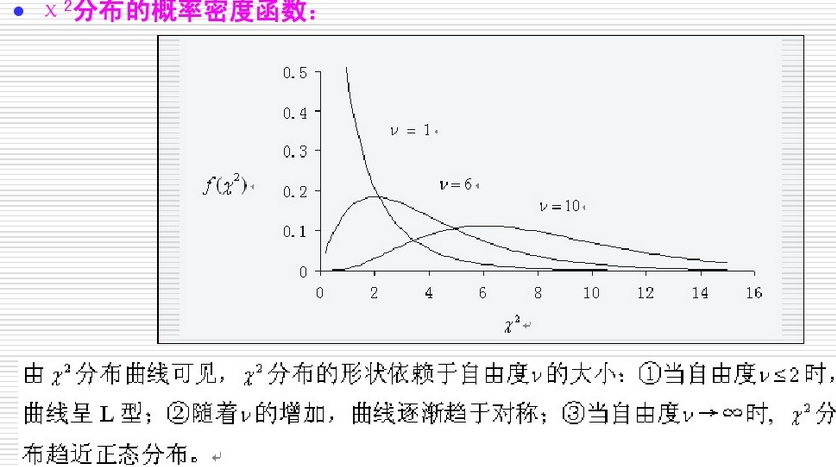
X²服從自由度為df=(r-1)(c-1)的卡方分佈。r,c是表中資料的行與列。
其中,卡方分佈即伽馬分佈函式如下
獨立性假設的概率:
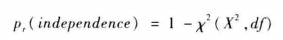
當概率值越小,標明兩個變數間獨立的概率越小,即兩變數間有很強的相關性。
上表資料對應的卡方統計量計算得:
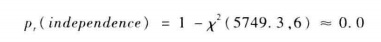
說明就業和居住狀況之間存在很強的相關性。
4.似然比檢驗統計量
兩個變數是名義變數
觀察樣本中計算的真實頻率分佈與已知概率總體分佈的差異:
兩個名義變數x,y的似然比統計量定義為:
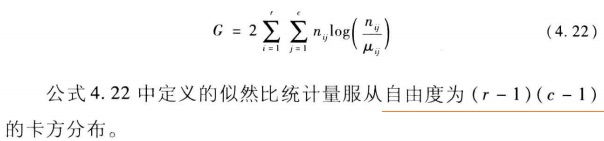
為何4.22公式是服從卡方分佈的???暫時不理解,先記下來。
那麼,通過似然比檢驗統計量可以得出兩個變數間的相關性,具體判斷類似卡方統計量。
5.概率比
兩個變數是名義變數。

如上表,
當變數x取x1時的違約比率odds=n11/n12;
當變數x取x2時的違約比率odds=n21/n22;
概率比的定義:
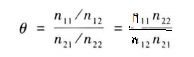
若概率比為1或趨近1,那麼兩個變數之間不存在相關性。
概率比在logistic迴歸建模製定打分卡起著關鍵作用。
6.F檢驗
F檢驗衡量一個連續變數與一個名義變數之間的關聯性。誰是因變數無所謂。
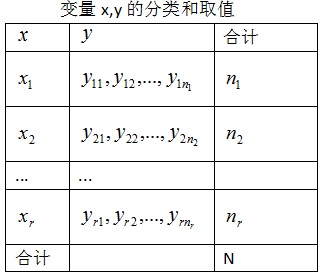
先舉例引入兩個引數MSTR,MSE,如下表:
p表示無關聯性的概率。p小表示,關聯性強。
7.基尼方差
基尼方差衡量三種情況的變數間的相關性:
1>一個連續變數,一個名義或順序變數;
2>兩個名義變數;
3>兩個順序變數。
考慮一個連續變數x和一個名義變數y的情況。基尼方差可以定義為:
G=1-SSE/STD
其中,SSE,STD見上。
8.熵方差
考慮一個類別變數x和一個連續y的情況。熵方差可以定義為:
E=1-SSE/STD
其中,SSE,STD見上。
關於基尼方差和熵方差,還不太明白。(參考《信用風險評分卡研究》)
9.資訊值
衡量兩個名義變數間的相關性,其中一個是二元的。比如x是名義變數,y是取兩個值0和1。

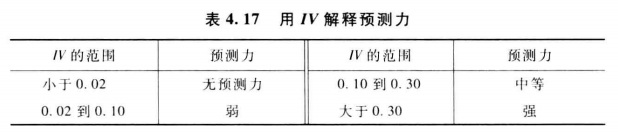
IV值,可以用於評估某個自變數(feature)對因變數(label)的預測能力,IV值越大預測能力越強。
後續在建立評分卡時,會進一步介紹IV值。