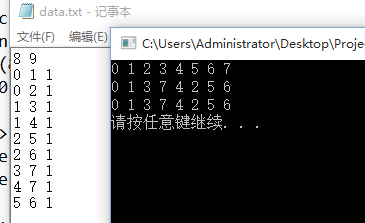
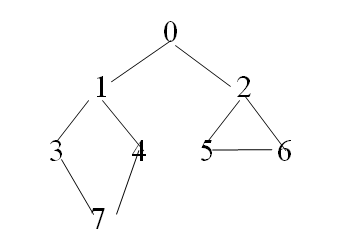
圖的BFS演算法和DFS的遞迴非遞迴演算法
阿新 • • 發佈:2019-01-01
#include<iostream> #include<fstream> #include<queue> #include<stack> using namespace std; #define MAX 10 typedef struct graph { int n; //頂點數 int e; //邊數 int edge[MAX][MAX]; //標識邊,0為沒有該邊,不為0則有邊,且標識邊的權值 }Graph; int visit[MAX] = { 0 }; //表示該頂點有沒有訪問過,沒有為0,有為1 void InitGraph(Graph *G) { for (int i = 0; i < MAX;i++) for (int j = 0; j < MAX; j++) (*G).edge[i][j] = 0; } //廣度優先搜尋演算法 void BFS(Graph G, int num) //num為從該點開始進行搜尋 { queue<int>Queue; cout << num <<" "; visit[num] = 1; Queue.push(num); //訪問完該點後入佇列 while (!Queue.empty()) //佇列不為空時 { num = Queue.front(); //出隊 Queue.pop(); for (int i = 0; i < G.n; i++) { if (G.edge[num][i] != 0 && visit[i] == 0) //找到與之相連的頂點入隊 { cout << i << " "; Queue.push(i); visit[i] = 1; } } } cout << endl; } void DFS1(Graph G, int num) //深度優先搜尋遞迴演算法 { int i; cout << num << " "; visit[num] = 1; for (i = 0; i < G.n; i++) { if (G.edge[num][i] != 0 && visit[i] == 0) DFS1(G, i); } } void DFS2(Graph G, int num) //深度優先搜尋非遞迴演算法 { stack<int> Stack; visit[num] = 1; Stack.push(num); while (!Stack.empty()) { num = Stack.top(); Stack.pop(); cout << num << " "; for (int i = G.n - 1; i >= 0; i--) { if (G.edge[num][i] != 0 && visit[i] == 0) { Stack.push(i); visit[i] = 1; } } } cout << endl; } int main() { int a, b, v, i; Graph G; ifstream cin("data.txt"); cin >> G.n >> G.e; //n,e為頂點個數,邊個數 InitGraph(&G); //對G進行初始化,整個MAX範圍初始化 for (i = 0; i < G.e; i++) //建圖 { cin >> a >> b >> v; //a,b為頂點,v為權值 G.edge[a][b] = v; G.edge[b][a] = v; } BFS(G, 0); //0為開始搜尋的頂點序號 for (i = 0; i < MAX; i++) visit[i] = 0; DFS1(G, 0); cout << endl; for (i = 0; i < MAX; i++) visit[i] = 0; DFS2(G, 0); system("pause"); return 0; }