十大經典資料探勘演算法:SVM
SVM(Support Vector Machines)是分類演算法中應用廣泛、效果不錯的一類。《統計學習方法》對SVM的數學原理做了詳細推導與論述,本文僅做整理。由簡至繁SVM可分類為三類:線性可分(linear SVM in linearly separable case)的線性SVM、線性不可分的線性SVM、非線性(nonlinear)SVM。
1.線性可分
對於二類分類問題,訓練集
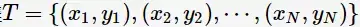
,其類別
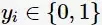
,線性SVM通過學習得到分離超平面(hyperplane):
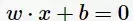
以及相應的分類決策函式:
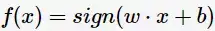
有如下圖所示的分離超平面,哪一個超平面的分類效果更好呢?
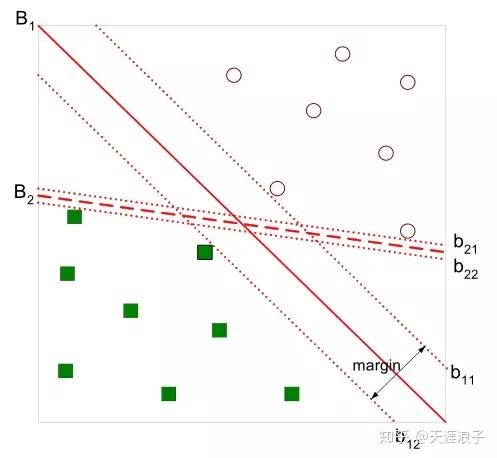
直觀上,超平面
![]()
的分類效果更好一些。將距離分離超平面最近的兩個不同類別的樣本點稱為支援向量(support vector)的,構成了兩條平行於分離超平面的長帶,二者之間的距離稱之為margin。顯然,margin更大,則分類正確的確信度更高(與超平面的距離表示分類的確信度,距離越遠則分類正確的確信度越高)。通過計算容易得到:
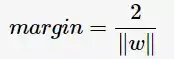
從上圖中可觀察到:margin以外的樣本點對於確定分離超平面沒有貢獻,換句話說,SVM是有很重要的訓練樣本(支援向量)所確定的。至此,SVM分類問題可描述為在全部分類正確的情況下,最大化
![]()
(等價於最小化
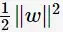
);線性分類的約束最優化問題

對每一個不等式約束引進拉格朗日乘子(Lagrange multiplier)
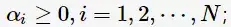
構造拉格朗日函式(Lagrange function):
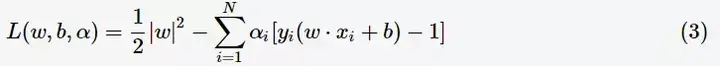
根據拉格朗日對偶性,原始的約束最優化問題可等價於極大極小的對偶問題:
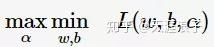
將
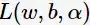
對
![]()
求偏導並令其等於0,則
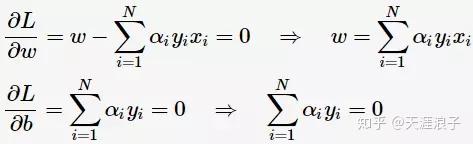
將上述式子代入拉格朗日函式(3)中,對偶問題轉為
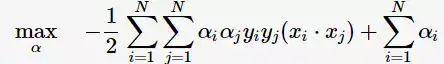
等價於最優化問
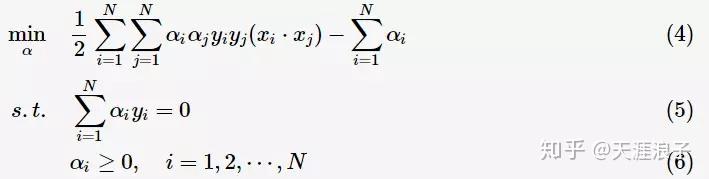
線性可分是理想情形,大多數情況下,由於噪聲或特異點等各種原因,訓練樣本是線性不可分的。因此,需要更一般化的學習演算法。
2.線性不可分
線性不可分意味著有樣本點不滿足約束條件(2),為了解決這個問題,對每個樣本引入一個鬆弛變數

這樣約束條件變為:
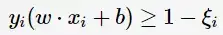
目標函式則變為
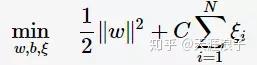
其中,
![]()
為懲罰函式,目標函式有兩層含義:
- margin儘量大,
- 誤分類的樣本點計量少
![]()
為調節二者的引數。通過構造拉格朗日函式並求解偏導(具體推導略去),可得到等價的對偶問題:
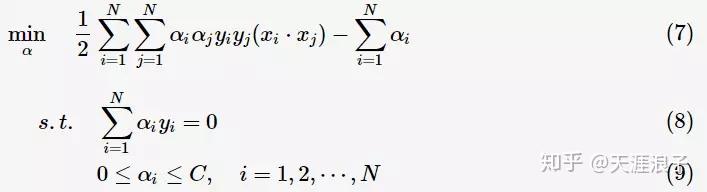
與上一節中線性可分的對偶問題相比,只是約束條件
![]()
發生變化,問題求解思路與之類似。
3.非線性
對於非線性問題,線性SVM不再適用了,需要非線性SVM來解決了。解決非線性分類問題的思路,通過空間變換ϕ(一般是低維空間對映到高維空間
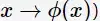
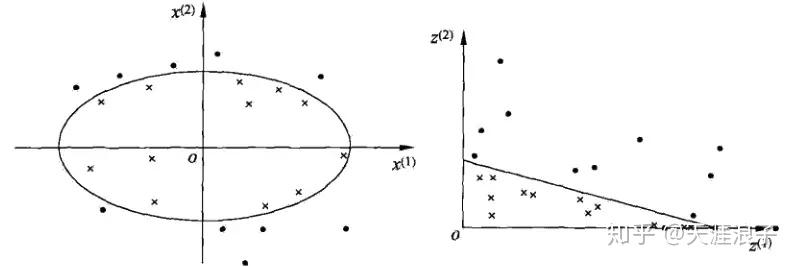
後實現線性可分,在下圖所示的例子中,通過空間變換,將左圖中的橢圓分離面變換成了右圖中直線。
在SVM的等價對偶問題中的目標函式中有樣本點的內積
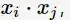
在空間變換後則是
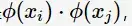
由於維數增加導致內積計算成本增加,這時核函式(kernel function)便派上用場了,將對映後的高維空間內積轉換成低維空間的函式:
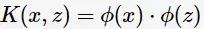
將其代入一般化的SVM學習演算法的目標函式(7)中,可得非線性SVM的最優化問題:
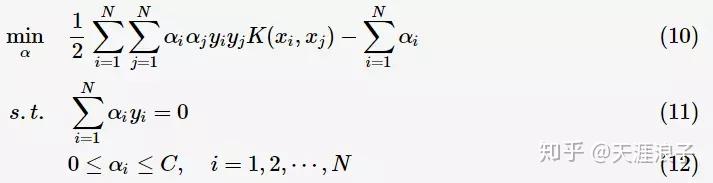
4.參考資料
[1] 李航,《統計學習方法》.
[2] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.
往期回顧:
