差一錯誤是所有程式設計師的噩夢！

它看起來是一個瑣碎的問題，卻非常煩人，許多程式設計師對它是採取一種“輕蔑”的態度，即使被它虐了千百遍，還是不願意正視這個問題。

其實，差一問題並不是一個小問題，我們應該對它給予足夠的重視。

在《C陷阱與缺陷》中，對這個問題有詳細的討論，這裡結合我的理解寫一寫解決這個問題的方法。

許多程式設計師在遇到差一問題時，常常採用的是“探測法”，一個位置應該寫n還是應該寫n-1，測試兩次就夠了，如果是兩個位置，就要測試四次，三個位置，要測試八次。。。

其中還可能存在“重疊錯誤”，當有兩個錯誤時，測試是正常的，當改正了一個錯誤，反而測試出錯。

一次過寫一段正確的程式碼，總比飛快得寫一堆糟糕程式碼，再做一天debug

正確的指標和下標，是計算出來的，不是亂蒙出來的！

指標運算

在學會計算指標之前，先要正確理解陣列和指標。

首先，地址就是一個整數，不是什麼神奇的東西！

指標是地址變數，陣列名是地址常量。

舉個例子,

int arr[10];

編譯器會分配10個整型大小的空間，首地址是arr，假設arr=500，那麼這個陣列就是這樣的：

其中能索引到的元素是arr[0]到arr[9],arr[n]也就是arr[10]是沒有的。

arr[0]有，arr[n]沒有，這個叫“不對稱邊界”，它帶來極大便利的同時，也引起了許多錯誤，不過，這種設計絕對是正確的。

可以用arr+5,表示第5個元素的地址（從0開始），但是不允許

指標也一樣，不同的是指標可以賦值。

地址量可以進行下列操作（p表示指標，i表示整型）：

p=p+i；    //指標後移i個位置

p=p-i; //指標前移i個位置

i=p1-p2; //兩個指標之間的元素個數

要指向p1和p2中間那個元素，可以用p0=p1+(p2-p1)/2,

用p0=(p1+p2)/2似乎也可以，不過編譯器不允許，因為p1+p2沒有意義。

問題解決

《C陷阱與缺陷》中，差一問題的解決方法，

一個是理解“不對稱邊界”，

另一個是“邊界計算”。

邊界計算，簡單舉個例子。

在一個位置，不知道應該寫n還是n-1，於是可以假設當n=2時，這裡應該寫1,所以，這個位置應該寫n-1。

“從1到10有幾個數？！”

“11個！”

“你給我想清楚！”

“11個！”

“那從1到2有幾個數？”

就是這樣了。

解決差一問題的方法絕不止這兩種，我們可以在實際問題的過程中，想到各種不同的方法。

二分查詢

下面以二分查詢為例，講解這個問題。

根據《程式設計珠璣》裡的資料，在100個專業程式設計師中，90%的程式設計師寫的二分查詢是存在bug的。

在沒有bug的二分查詢程式碼中，也可能存在元素的重複比較。

我寫的二分查詢是這樣的：

int* bs(int* arr,int n,int x){

⓪ if(n==0)return NULL;

① else if(x==arr[n/2])return arr+n/2;

② else if(x<arr[n/2])return bs(arr,n/2,x);

③ else return bs(arr+n/2+1,n-n/2-1,x);

}

元素按從小到大的順序排，如果找到，返回的是元素的地址，找不到則返回NULL。（如果找到了bug，請告訴我）。

我寫這段程式碼的過程是這樣的：

先在紙上畫出記憶體模型

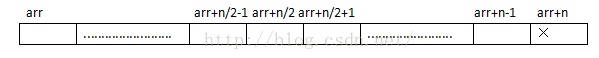
⓪語句，當陣列沒有元素了，就返回NULL

①語句，比較x是否等於arr[n/2],(這裡arr[n/2]是不是正中間的元素並不重要），如果等於，返回它的地址，arr+n/2

②語句，比較x是否小於arr[n/2],如果小於，應該繼續查詢的是位於arr[n/2]前面的那一段陣列，不包括arr[n/2]，因此，這段陣列的首地址還是arr，它的最後一個元素是arr[n/2-1],長度是n/2

③語句，應該繼續查詢的是位於arr[n/2]後面的那一段陣列，不包括arr[n/2]，因此，這段陣列的首地址是arr+n/2+1,那麼長度應該怎麼計算呢？

第1個方法：右邊陣列長度=原陣列長度-左邊陣列長度-arr[n/2]這個元素

=n-n/2-1

第2個方法：右邊陣列的末地址=原陣列的末地址

右邊陣列的首地址+長度=原陣列的首地址+長度

arr+n/2+1+m=arr+n

m=n-n/2-1

所以，右邊陣列的長度為n-n/2-1（n-n/2不一定等於n/2,因為整數除法是向下取整的)

待定係數法

我想到的另一個方法，是待定係數法。

以對稱矩陣的壓縮儲存為例，講解這個方法。

對稱矩陣的壓縮儲存是資料結構考試中的必備題目，在各大考試中頻繁露面。

在不同的試題中，具體細節也不同，有的儲存上三角，有的儲存下三角，有的從0開始，有的從1開始，還有些是01混合。

上試題：

一個10階對稱矩陣A，採用行優先順序壓縮儲存“下三角元素”，a[1,1]為第一個元素，其儲存地址為陣列B[0]，每個元素佔有1個儲存地址空間，則a[ i, j ]的地址為_________。

解法：

先畫出矩陣的一部分

設B[t]對應a[ i, j ]，即對應方程為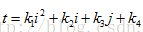，選出四個元素

當i=1,j=1時，t=0

當i=2,j=1時，t=1

當i=3,j=1時，t=3

當i=3,j=2時，t=4

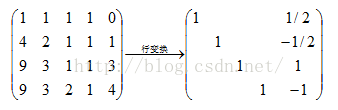
寫成矩陣形式可以更好計算：

即，

則a[ i, j ]的地址為。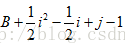

這裡需要注意的是，選取元素時不能取同一條直線上的元素，否則在計算時矩陣不滿秩，得不到最後結果。