矩陣的特徵分解非常好理解，假設現在有一個NxN的矩陣A，如果這個矩陣A有N個線性無關的特徵向量，那麼A就可以分解為

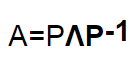
P代表NxN的方陣，中間的Λ 代表對角矩陣

怎麼理解呢？為什麼可以分解成這樣呢？

其實這個就是矩陣相似對角化的變形而已！

我們首先來複習一下矩陣相似對角化的基本概念

對角矩陣 ： 對角矩陣是指只有主對角線上含有非零元素的矩陣,一般記作：Λ ，例如：

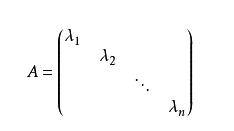
矩陣相似：若矩陣A和矩陣B都是n階矩陣，如果存在可逆矩陣P，使得：

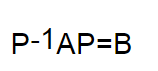
則稱矩陣A和B相似，記作A~B

矩陣相似對角化：如果一個n階矩陣A有n個線性無關的特徵向量，那麼矩陣A與由其特徵值所組成的對角矩陣相似，即：

A~Λ

所以現在我們再回來看特徵分解的意思

1.有一個NxN的矩陣A （說明這個矩陣是一個方陣）
2.這個矩陣A有N個線性無關的特徵向量 （說明這個矩陣A可以相似對角化）

所以有：

A~Λ

由矩陣相似的定義有：

把左邊的P變換到右邊去，則有

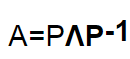
所以矩陣的特徵分解是實質上只是矩陣相似對角化形式的一個變形而已！