import numpy as np
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

# 目標函式
def real_func(x):
    return np.sin(2*np.pi*x)

# 多項式
def fit_func(p, x):
    f = np.poly1d(p)
    return f(x)

# 殘差
def residuals_func(p, x, y):
    ret = fit_func(p, x) - y #注意此處沒有平方
    return ret

regularization = 0.0001

#正則化之後的殘差
def residuals_func_regularization(p, x, y):
    ret = fit_func(p, x) - y
    ret = np.append(ret, np.sqrt(0.5*regularization*np.square(p))) # L2範數作為正則化項
    return ret


# 十個點'
x = np.linspace(0, 1, 10)
x_points = np.linspace(0, 1, 1000)
# 加上正態分佈噪音的目標函式的值
y_ = real_func(x)
y = [np.random.normal(0, 0.1) + y1 for y1 in y_]

index = 0
plt.figure(figsize=(15, 8))

def fitting(M=0):
    """
    M    為 多項式的次數
    """
    # 隨機初始化多項式引數
    p_init = np.random.rand(M + 1)
    # 最小二乘法
    p_lsq = leastsq(residuals_func, p_init, args=(x, y))
    #p_lsq = leastsq(residuals_func_regularization, p_init, args=(x, y)) #加入正則化
    print('Fitting Parameters:', p_lsq[0])

    # 視覺化
    plt.subplot(141 + index)
    plt.plot(x_points, real_func(x_points), label='real')
    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
    plt.plot(x, y, 'bo', label='noise')
    plt.legend()
    return p_lsq



for i in [0, 1, 3, 9]:
    lsq_0 = fitting(i)
    index += 1

plt.subplots_adjust(top=0.92, bottom=0.08, left=0.10, right=0.95, hspace=0.25,
                        wspace=0.35) #調整子圖間距

plt.savefig("demo.jpg")
plt.show()
 

正則化前

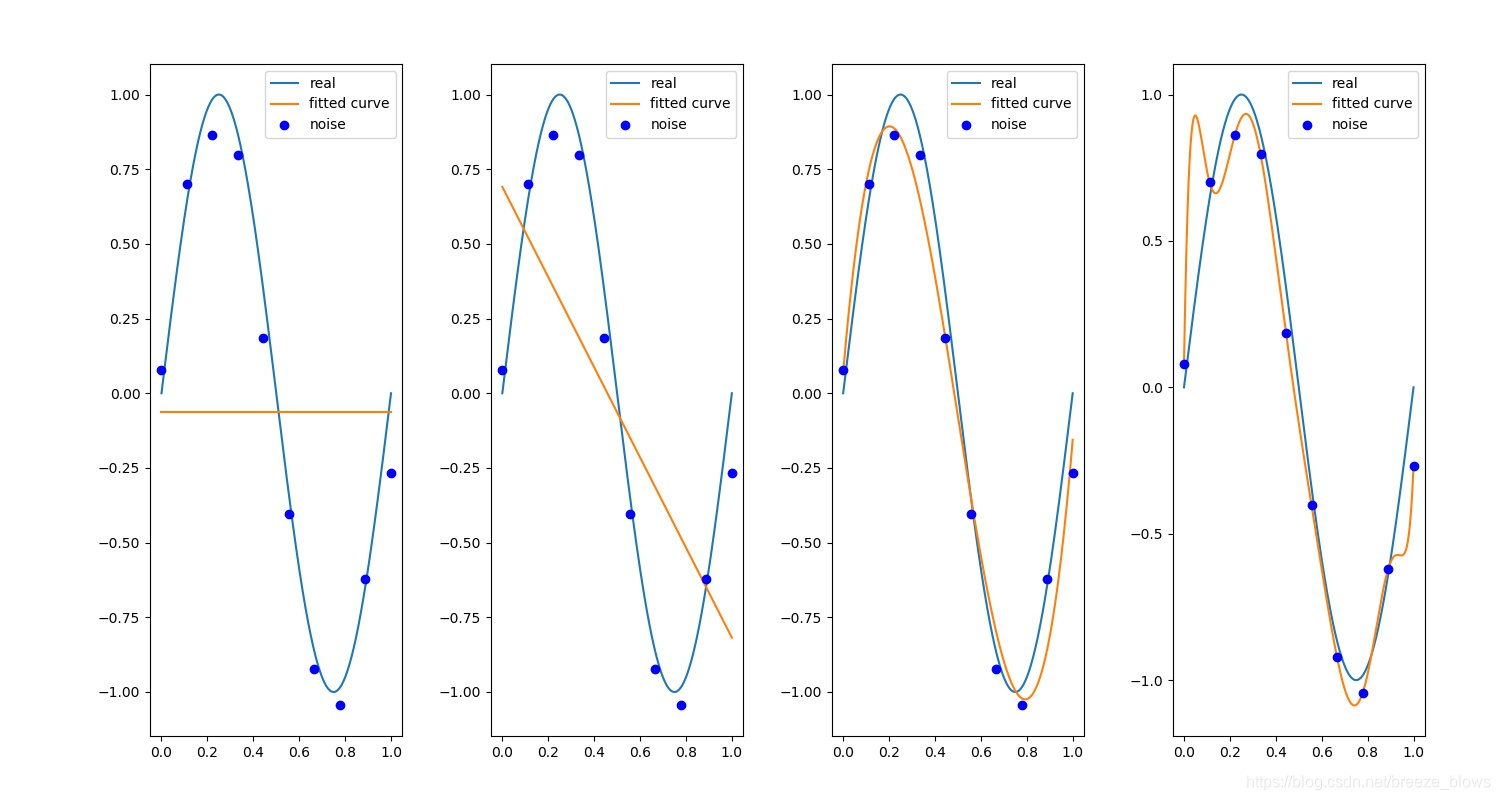
正則化後

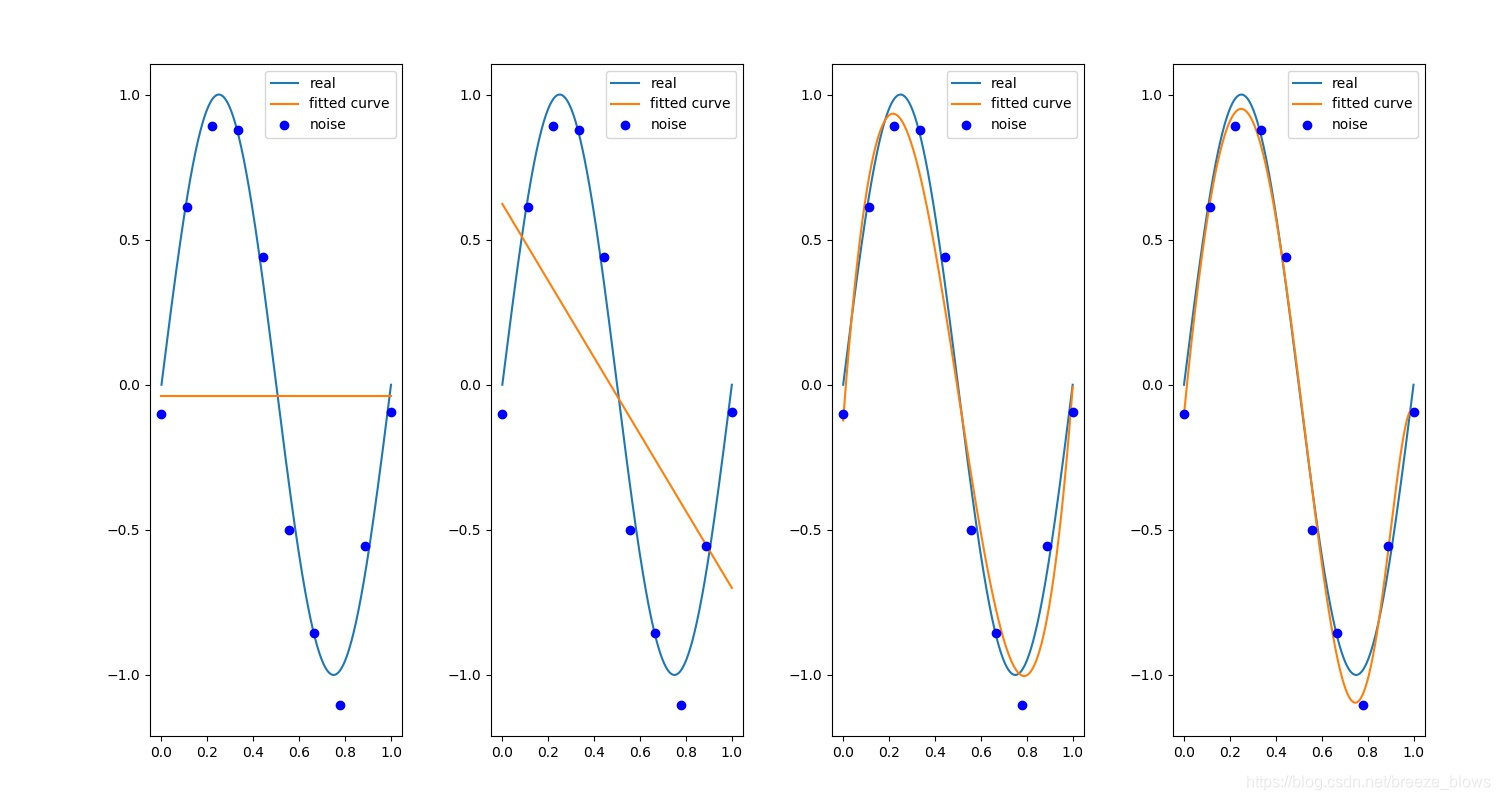
可以明顯看出正則化的作用