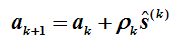梯度上升法,梯度下降法
阿新 • • 發佈:2019-01-02
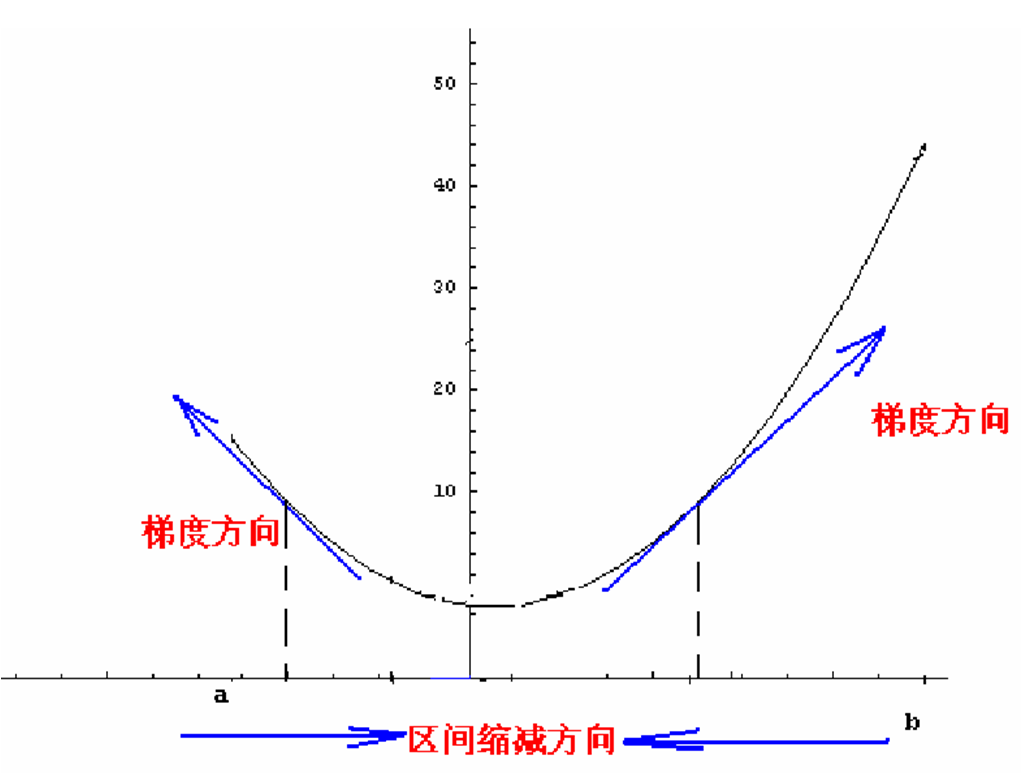
一個多元函式的梯度方向是該函式值增大最陡的方向。
例如求二次函式的最小值,這裡採用梯度下降法:
梯度下降法的思想:假設現在要求上圖中函式f(x)的最小值,先選擇一個初始點,下一個點的產生是沿著梯度直線方向(本函式求最小值是沿著梯度負方向,若求最大值則沿著梯度方向)
為什麼叫梯度上升和梯度下降呢?個人理解是沿著梯度的方向上升(向上走)叫梯度上升,沿著梯度的方向下降(向下走)叫梯度下降。那這裡的梯度是什麼呢?
梯度上升法的基本思想是:要找到某函式的最大值,最好的方法是沿著該函式的梯度方向探尋。
什麼意思,舉個例子,假如你想以最快的速度爬到山頂,你應該怎樣選擇每一步,答案是選擇坡度較陡的地方,越陡峭的地方,上升就越快,如果你沿著山上的公路往山頂走肯定是最慢的,因為公路一般都是之字形坡度較緩。同理可有梯度下降,法梯度下降法,就是利用負梯度方向來決定每次迭代的新的搜尋方向,使得每次迭代能使待優化的目標函式逐步減小。
下面給出梯度下降法的迭代公式:
其中的引數:
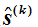 表示梯度的負方向
表示梯度的負方向 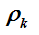 表示步長
表示步長 公式的意思是:下一個點是由當前點向
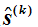 方向移動
方向移動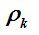
思考:梯度下降法,梯度上升法在分類資料點時為什麼能起作用?