從2017.3.15到2017.4.6，花費三個星期的時間投入到2017華為精英挑戰賽。我是第一次參加這種類似於ACM的演算法競賽，雖然成績從最初前32強最後跌出64強無緣複賽，但是真的學到了很多東西。大神好多，高手如雲，繼續努力！

在此分享一下比賽心得，總結在這次挑戰賽中所做的努力和工作：

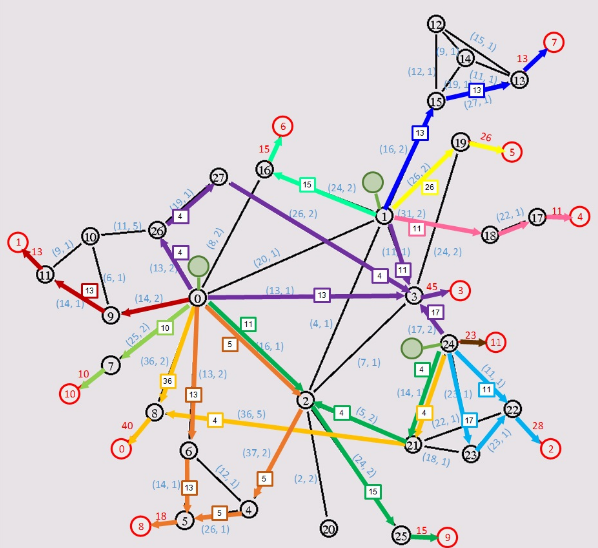
上圖為G省網路拓撲圖，黑色圓圈為網路節點，紅色圓圈為消費節點，圓圈內的數字為節點編號。節點之間的連線為網路鏈路。鏈路上的標記(x, y)中，x表示鏈路總頻寬（單位為Gbps），y表示每Gbps的網路租用費。消費節點相連鏈路上的數字為消費節點的頻寬消耗需求（單位為Gbps）。

現在假設需要在該網路上部署視訊內容伺服器，滿足所有消費節點的需求。一個成本較低的方案如下圖所示（選擇0,1,24作為伺服器），其中綠色圓圈表示已部署的視訊內容伺服器，通往不同消費節點的網路路徑用不同顏色標識，並附帶了佔用頻寬的大小：

通過分析賽題我們小組發現可以總結為以下幾個問題：

1.當選定伺服器位置時，如何制定給消費節點提供頻寬的策略？

舉例：如圖中，選擇0,1,24作為伺服器，如何制定策略在滿足所有消費節點頻寬需求的前提下，使所花費用最小。

2.如何選擇伺服器的位置？

l 初始伺服器位置選擇問題

l 更新伺服器位置策略問題

解答：

針對問題1：

採用最小費用最大流的方法(該演算法用來解決從一個點到另一個點，提供頻寬最大時，所需的最小費用)，將所有伺服器連向一個超級伺服器(源點)，將所有消費節點連向一個超級消費節點(匯點)。例如：選擇伺服器0,1,24時，連線方案如下圖所示。注意：源點到伺服器頻寬無限，費用為0，單向傳輸；消費節點到匯點頻寬為自身所需頻寬，費用為0，單向傳輸

如果不這樣連線和考慮問題，在計算時會遇到計算邏輯複雜和計算速度慢的問題。通過不斷地優化，我們最終在資料規模達到網路節點800點、消費節點360點時，計算一次費用流只需10ms左右。

針對問題2：

方法1：這個賽題明顯是一個NP-Hard問題，最開始我們想用暴力的方法解決，首先與每個消費節點直接相連線的網路節點放置局伺服器(即初始伺服器位置選擇，因為這樣一定可以保證有解)

方法2：由於當資料規模增大到一定程度時，方法1的演算法無法在題目要求的90s內收斂，所以要求一個更快的收斂方案。第二個方法還是利用直連的方法佈局初始伺服器集合，而我們只在當前與消費節點直連伺服器中隨機減一個或者換一個，直到收斂，取最少費用的一次伺服器佈局。這樣我們相當於將原來在800個點的網路節點中搜索解，轉化為了在360個消費節點直連的網路節點中搜索點，顯然我們的演算法無法找到全域性最優解，但是這樣可以在有限的時間內更快的收斂，達到一個更小的費用。 由於一直在直連網路節點中搜索，所以對伺服器單價不高的情況還是有不錯的解的。並且因為一直在直連中計算費用流，在規定時間內計算費用流時間縮減了很多，所以在大案例中有不錯的解。大案例(800網路節點)中我們測試得出迭代次數可以多達3萬多次，而第一種方法僅有3000多次，快了10倍。在大案例中追求有限時間內搜尋最優解還是很不錯的idea，得益於此在大規模的比賽樣例中我們取得了不錯的成績。

方法3：其實很明顯，上面兩種方法都會遇到跳不出區域性最優解的問題，一旦我們陷入一個區域性最優解根本跳不出去，顯然還是需要一個啟發式的方法，經典的演算法像蟻群，爬山，模擬退火，遺傳演算法，粒子群等，大家可以查閱相關論文，這些都是經典TSP問題很好的解決方法，用在這裡肯定也是可行的。 我們最後在伺服器選址使用的是模擬退火，演算法簡單又快速，這也是我們第三種演算法。第三種方法初始化還是使用的直連的方法，每次隨機加一個伺服器、減一個或者換一個，但是我們並不是將這個概率設死，不是對當前花費沒有減小的效果就捨棄這次抉擇，而是以一定概率去接受它，並且這個概率隨著迭代深入慢慢減小，這就是經典的模擬退火的演算法，一定程度上可以避免陷入區域性最優。

待實現的方法：

　　但是很遺憾，想法是挺好的，由於沒有經驗，經過兩天調參我們的效果還是不理想，沒有解決陷入區域性最優的困局。直到比賽結束這個問題也沒有解決，最後很遺憾沒有進入複賽。

　　其實解決區域性最好方法就是增加隨機性，一個是選擇伺服器的時候加大隨機性，這裡rand()所以使用時間作為srand引數自然是最好的。

另外初始伺服器的隨機性，所以一旦結果收斂我們應該重啟再繼續搜尋，但是很遺憾這個方法我們沒有時間實踐了，就是伺服器佈局不要選擇直連，而是全域性隨機選擇跟消費節點數量相同的伺服器，然後多次抉擇直到收斂。

最後還有一個思想是經過模擬退火後，接受概率會越來越小，陷入區域性最優解。之後我們應該將溫度重新升溫，即接受概率恢復到某一值，重新降溫，如此反覆。

我覺得我們失敗就是敗在了這裡，有些遺憾，在最後才想明白。其它人的方法我就不知道，可能還有一些比較啟發的選擇方法，我們另外還根據每個網路節點的出度設計每個網路節點選擇為伺服器的權重，自然出度大情況我們更希望它被選擇為伺服器，但最終效果也不盡如人意。等比賽結束看看大神們的程式碼，膜拜一下，再重新思考一下該問題。

我們所做過的優化案例：

　　整個過程，我們對演算法做了很多優化，雖然我們沒有逃出區域性最優解的困局，但是我敢說我們最小費用和整個演算法優化是頂尖的。看討論群裡他們分享的速度都沒有我們的快。

　   主要有以下的優化：

1、費用流計算中不管中間路線佈局，我們將多源多匯問題優化為單元對單元，也就是模擬設計兩個超級節點，一個連線所有伺服器，一個連線所有消費節點，整個過程簡化為單源單匯費用流問題；

2、每迭代一次不必重新載入所有圖資料，我們採用個別資料還原再重新進行下一輪的最小費用流計算即可；

3、伺服器集合儲存的時候，我們採用標準模板庫中set資料結構其實是最好的，第一伺服器不會重複set很符合這個性質，第二set是基於紅黑樹實現的，插入刪除很快速，所以使用set比其他任何資料結構都要好，這個設計又讓我們的演算法效率提高了不少；

4、在各種迴圈中，應考慮其提前終止的情況，避免沒有意義的計算。

以上就是我的總結，雖然很遺憾沒有進入複賽，但是過程還是學習了不少，繼續加油！