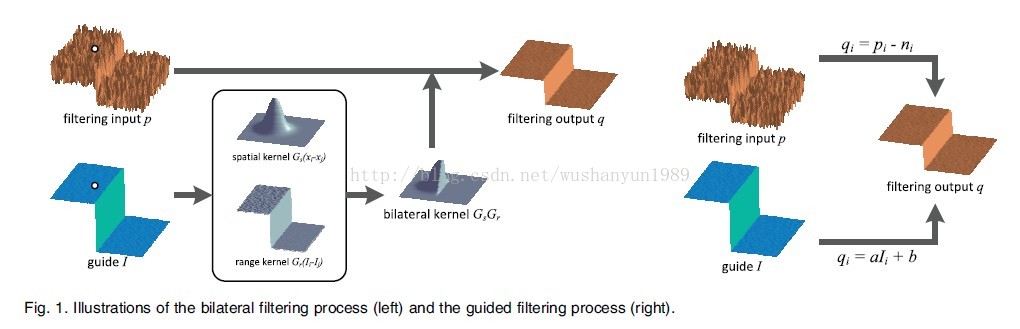
從原理上分析，這幾種濾波器沒有太大的差別，都是基於最基本的思想：在梯度比較大的地方（edges）實現preserve，要求儘量不進行平滑，最好是輸出與輸入一樣；而在梯度比較小的地方，儘量的平滑一下，輸入與輸出可以有稍大的不同！

那麼從這個原理出發，我們來推導雙邊濾波和引導濾波：

對於雙邊濾波的話，將spatial kernel（也就是gaussian kernel）與range kernel（也就是intensity的相似性權重）分別提取出來，之後合併為bilateral kernel，也就是Gs×Gr，之後與待濾波的輸入影象進行卷積濾波，也就得到了濾波後的影象，引入gaussian kernel無可厚非，主要是為了進行平滑濾波，而引入range kernel主要是為了實現上面那句在梯度較大的地方，我們不進行平滑，而梯度較大的地方，那個range kernel G

r比較小，也就是抑制了Gs的作用，實現平坦區域平滑濾波，邊沿區域保持的目的！

對於引導和加權最小二乘，都可以直接從最優化手段入手，只不過表現形式不同而已：

min(Iin−Iout)2+λ(regularitem)
不同在於regular item以及Iout的設計上。

加權最小二乘直接使用水平方向和豎直方向的梯度作為正則項，懲罰因子，採用矩陣形式進行描述，然後進行推導得到對應的平滑係數，之後直接得到矩陣求逆運算得到Iwls。

引導濾波器則是用線性表示的方法得到輸出Igif，同樣採用上面的最小化方法，不過選擇的正則項是線性係數ak。之所以採用線性的表示方法，是出於畫素的區域性性，區域性線性關係肯定是存在的。同時為了保證在邊緣地區進行保持，在平坦區域進行平滑的目的，選擇線性係數a

k作為正則項，如果ak=0，很明顯輸出直接全平了，如果ak=1，bk=0，輸入等於輸出，很顯然邊緣完全保持了。這個求解方法讓我想起了支撐向量機中的推導過程，也是懲罰項的巧妙設計。所以，最優化函式前面的一項用來保證邊緣，而後一項需要用來保證平滑性。也就是說，兩者應該是矛盾，前一項大的話，後一項必須被約束很小才行，所以也就是說如果輸入與輸出相差較大的話，主要發生在ak很小的地方，也就是比較平滑的地方；而輸出與輸出相差較小的話，主要發生在ak比較大的地方，最大為1，也就是比較不平滑，邊緣地方。反過來控制正則項，去考察前面一項也能得到類似的結論。

最後得出的結論從上面總結的可以看出：

（1）High
 
 variance的區域，$a_k$趨向於1，$b_k$趨向於0，從而邊緣保持；
（2）Low variance的區域，$a_k$趨向於0，$b_k$趨向於均值，從而進行平滑；

具體的實現，可以參看對應的程式碼，在E:\LabProject\InfraredImageProcessingAlgorithms中都有相關的參考例子。

2016-7-3 20:51
張朋藝 [email protected]