強化學習實踐一 :迭代法評估4*4方格世界下的隨機策略
本篇用程式碼演示David Silver《強化學習RL》第三講 動態規劃尋找最優策略中的示例——方格世界,即用動態規劃演算法通過迭代計算來評估4*4方格世界中的一個隨機策略。具體問題是這樣:
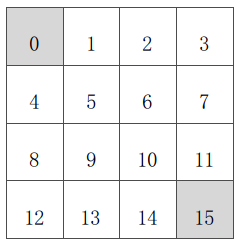
已知(如上圖):
- 狀態空間 S:
為非終止狀態;
,
終止狀態,圖中灰色方格所示兩個位置;
- 行為空間 A:{n, e, s, w} 對於任何非終止狀態可以有向北、東、南、西移動四個行為;
- 轉移概率 P:任何試圖離開方格世界的動作其位置將不會發生改變,其餘條件下將100%地轉移到動作指向的位置;
- 即時獎勵 R:任何在非終止狀態間的轉移得到的即時獎勵均為-1,進入終止狀態即時獎勵為0;
- 衰減係數 γ:1;
- 當前策略π:個體採用隨機行動策略,在任何一個非終止狀態下有均等的機率往任意可能的方向移動,即π(n|•) = π(e|•) = π(s|•) = π(w|•) = 1/4。
問題:評估在這個方格世界裡給定的策略。
該問題等同於:求解該方格世界在給定策略下的(狀態)價值函式,也就是求解在給定策略下,該方格世界裡每一個狀態的價值。
我們使用Python編寫程式碼解決該問題。
- 宣告狀態
S = [i for i in range(16)]- 宣告行為空間
A = ['n','e', 's', 'w']- 結合方格世界的佈局特點,簡易宣告行為對狀態的改變
ds_actions = {"n": -4, "e": 1, "s": 4, "w": -1}- 環境動力學
模擬小型方格世界的環境動力學特徵:
Args:
s 當前狀態int 0 - 15
a 行為 str in ['n','e','s','w'] 分別表示北、東、南、西
Returns: tuple (s_prime, reward, is_end)
s_prime 後續狀態
reward 獎勵值
is_end 是否進入終止狀態def dynamics(s, a): # 環境動力學 s_prime = s if (s % 4 == 0 and a== 'w') or (s < 4 and a == 'n') or ((s + 1) % 4 == 0 and a == 'e') or (s > 11 and a == 's') or s in [0, 15]: pass else: ds = ds_actions[a] s_prime = s + ds reward = 0 if s in [0, 15] else -1 is_end = True if s in [0, 15] else False return s_prime , reward, is_end
def P(s, a, sl):# 狀態轉移概率函式
s_prime, _, _ = dynamics(s, a)
return sl == s_primedef R(s, a):# 獎勵函式
_, r, _ = dynamics(s, a)
return rgamma = 1.00
MDP = S, A, R, P, gamma 最後建立的MDP 同上一章一樣是一個擁有五個元素的元組,只不過 R 和 P 都變成了函式而不是字典了。同樣變成函式的還有策略。下面的程式碼分別建立了均一隨機策略和貪婪策略,並給出了呼叫這兩個策略的統一的介面。由於生成一個策略所需要的引數並不統一,例如像均一隨機策略多數只需要知道行為空間就可以了,而貪婪策略則需要知道狀態的價值。為了方便程式使用相同的程式碼呼叫不同的策略,我們對引數進行了統一。
def uniform_random_pi(MDP = None, V = None, s = None, a = None): # 均一隨機策略
_, A, _, _, _ = MDP
n = len(A)
return 0 if n == 0 else 1.0/ndef greedy_pi(MDP, V, s, a):# t貪婪策略
S, A, P, R, gamma = MDP
max_v, a_max_v = -float('inf'), []
for a_opt in A:# 統計後續狀態的最大價值以及到達到達該狀態的行為( 可能不止一個)
s_prime, reward, _ = dynamics(s, a_opt)
v_s_prime = get_value(V, s_prime)
if v_s_prime > max_v:
max_v = v_s_prime
a_max_v = [a_opt]
elif(v_s_prime == max_v):
a_max_v.append(a_opt)
n = len(a_max_v)
if n == 0: return 0.0
return 1.0/ n if a in a_max_v else 0.0def get_pi(Pi, s, a, MDP = None, V = None):
return Pi(MDP, V, s, a)在編寫貪婪策略時,我們考慮了多個狀態具有相同最大值的情況,此時貪婪策略將從這多個具有相同最大值的行為中隨機選擇一個。為了能使用前一章編寫的一些方法,我們重寫一下需要用到的諸如獲取狀態轉移概率、獎勵以及顯示狀態價值等的輔助方法:
# 輔助函式
def get_prob(P, s, a, sl):
return P(s, a,sl)
def get_reward(R, s, a):
return R(s, a)
def set_value(V, s, v):
V[s] = v
def get_value(V, s):
return V[s]
def display_V(V):
for i in range(16):
print('{0:>6.2f}'.format(V[i]),end = '')
if (i + 1) % 4 == 0:
print('')
print()有了這些基礎,接下來就可以很輕鬆地完成迭代法策略評估、策略迭代和價值迭代了。在前一章的實踐環節,我們已經實現了完成這三個功能的方法了,這裡只要做少量針對性的修改就可以了,由於策略Pi 現在不是查表式獲取而是使用函式來定義的,因此我們需要做相應的修改,修改後的完整程式碼如下:
def compute_q(MDP, V, s, a):
#根據給定的MDP, 價值函式V, 計算狀態行為對s,a的價值qsa
S, A, R, P, gamma =MDP
q_sa = 0
for s_prime in S:
q_sa += get_prob(P, s, a, s_prime) * get_value(V, s_prime)
q_sa = get_reward(R, s, a) + gamma * q_sa
return q_sadef compute_v(MDP, V, Pi, s):
# 給定MDP下依據某一策略Pi和當前狀態價值函式V計算某狀態s的價值
S, A, R, P, gamma = MDP
v_s = 0
for a in A:
v_s += get_pi(Pi, s, a, MDP, V) * compute_q(MDP, V, s, a)
return v_sdef update_V(MDP, V, Pi):
# 給定一個MDP和一個策略, 更新該策略下的價值函式V
S, _, _, _, _ = MDP
V_prime = V.copy()
for s in S:
set_value(V_prime, s, compute_v(MDP, V_prime, Pi, s))
return V_primedef policy_evaluate(MDP, V, Pi, n):
# 使用n次迭代計算來評估一個MDP在給定策略Pi下的狀態價值, 初始時價值為V
for i in range(n):
V = update_V(MDP, V, Pi)
return Vdef policy_iterate(MDP, V, Pi, n, m):
for i in range(m):
V = policy_evaluate(MDP, V, Pi, n)
Pi = greedy_pi # 第一次迭代產生新的價值函式後隨機使用貪婪策略
return V# 價值迭代得到最優狀態價值過程
def compute_v_from_max_q(MDP, V, s):
# 根據一個狀態的下所有可能的行為價值中最大一個來確定當前狀態價值
S, A, R, P, gamma = MDP
v_s = -float('inf')
for a in A:
qsa = compute_q(MDP, V, s, a)
if qsa >= v_s:
v_s = qsa
return v_sdef update_V_without_pi(MDP, V):
# 在不依賴策略的情況下直接通過後續狀態的價值來更新狀態價值
S, _, _, _, _ = MDP
V_prime = V.copy()
for s in S:
set_value(V_prime, s, compute_v_from_max_q(MDP, V_prime, s))
return V_primedef value_iterate(MDP, V, n):
# 價值迭代
for i in range(n):
V = update_V_without_pi(MDP, V)
return V策略評估
接下來就可以來呼叫這些方法進行策略評估、策略迭代和價值迭代了。我們先來分別評估一下均一隨機策略和貪婪策略下16 個狀態的最終價值:
V = [0 for _ in range(16)]# 狀態價值
V_pi = policy_evaluate(MDP, V, uniform_random_pi, 100)
display_V(V_pi)
V = [0 for _ in range(16)]# 狀態價值
V_pi = policy_evaluate(MDP, V, greedy_pi, 100)
display_V(V_pi)
V = [0 for _ in range(16)]# 狀態價值
V_pi = policy_evaluate(MDP, V, uniform_random_pi, 100)
display_V(V_pi)
V = [0 for _ in range(16)]# 狀態價值
V_pi = policy_evaluate(MDP, V, greedy_pi, 100)
display_V(V_pi)
# 輸出結果
0.00-223.96-319.95-351.94
-223.96-287.95-319.95-319.95
-319.95-319.95-287.96-223.97
-351.94-319.95-223.97 0.00
0.00-16.00-32.00-48.00
-16.00-32.00-48.00-32.00
-32.00-48.00-32.00-16.00
-48.00-32.00-16.00 0.00可以看出,均一隨機策略下得到的結果與圖3.5 顯示的結果相同。在使用貪婪策略時,各狀態的最終價值與均一隨機策略下的最終價值不同。這體現了狀態的價值是基於特定策略的。
策略迭代
編寫如下程式碼進行貪婪策略迭代,觀察每迭代1 次改善一次策略,共進行100 次策略改善
後的狀態價值:
V = [0 for _ in range(16)]# 重置狀態價值
V_pi = policy_iterate(MDP, V, greedy_pi, 1, 100)
display_V(V_pi)
0.00-16.00-32.00-48.00
-16.00-32.00-48.00-32.00
-32.00-48.00-32.00-16.00
-48.00-32.00-16.00 0.00價值迭代
下面的程式碼展示了單純使用價值迭代的狀態價值,我們把迭代次數選擇為4 次,可以發現僅4 次迭代後,狀態價值已經和最優狀態價值一致了。
V_star = value_iterate(MDP, V, 4)
display_V(V_star)
#輸出結果
0.00-16.00-32.00-48.00
-16.00-32.00-48.00-32.00
-32.00-48.00-32.00-16.00
-48.00-32.00-16.00 0.00
我們還可以編寫如下的程式碼來觀察最優狀態下對應的最優策略:
def greedy_policy(MDP, V, s):
S, A, P, R, gamma = MDP
max_v, a_max_v = -float('inf'),[]
for a_opt in A:
# 統計後續狀態的最大價值以及到達到達該狀態的行為( 可能不止一個)
s_prime, reward, _ = dynamics(s, a_opt)
v_s_prime = get_value(V, s_prime)
if v_s_prime > max_v:
max_v = v_s_prime
a_max_v = a_opt
elif(v_s_prime == max_v):
a_max_v += a_opt
return str(a_max_v)
def display_policy(policy, MDP, V):
S, A, P, R, gamma = MDP
for i in range(16):
print('{0:^6}'.format(policy(MDP, V, S[i])), end = ' ')
if (i + 1) % 4 == 0:
print('')
print()
display_policy(greedy_policy, MDP, V_star)
# 輸出結果
nesw w w sw
n nw nesw s
n nesw es s
ne e e nesw
上面分別用n,e,s,w 表示北、東、南、西四個行為。這與圖3.5 顯示的結果是一致的。讀者可以通過修改不同的引數或在迭代過程中輸出價值和策略觀察價值函式和策略函式的迭代過程。
