這一篇部落格主要是與狀態篇形成互補。主要記下一些面試中的題目，並給出題解。
作者注：所有的題目都只給出思考方法，不給出程式碼。

筆試：

Q：給出一篇英語文章，並統計裡面每個單詞的出現次數。

A：這題，我用OC給出了一個解法。就是用字典，< key, value >中的key為單詞名，value為單詞出現的次數，通篇掃描一次文章，那麼字典裡就存了每個單詞出現的次數。
這是個可行的辦法，但是這樣子呢，就使用了蘋果的庫裡的東西——NSDictionary，那麼在筆試完成後，我和朋友討論這個問題，朋友給出了一個更為亮眼的解法，下面來解釋一下思路。
其實就是，朋友構建了一個字典樹（Trie樹）。
我按照朋友的意思，大概還原了一下節點結構體的模樣：

struct Node {
    char c;
    int count; //統計當前單詞出現的次數
    Node *sib; //兄弟節點的指標
    Node *next; //進入到下一個層級的節點的指標
};

下面給出一個英文語句：I am going to drink a cup of coffee.
針對這句話，我手繪了生成的Trie樹的一部分，希望能表達清楚意思：

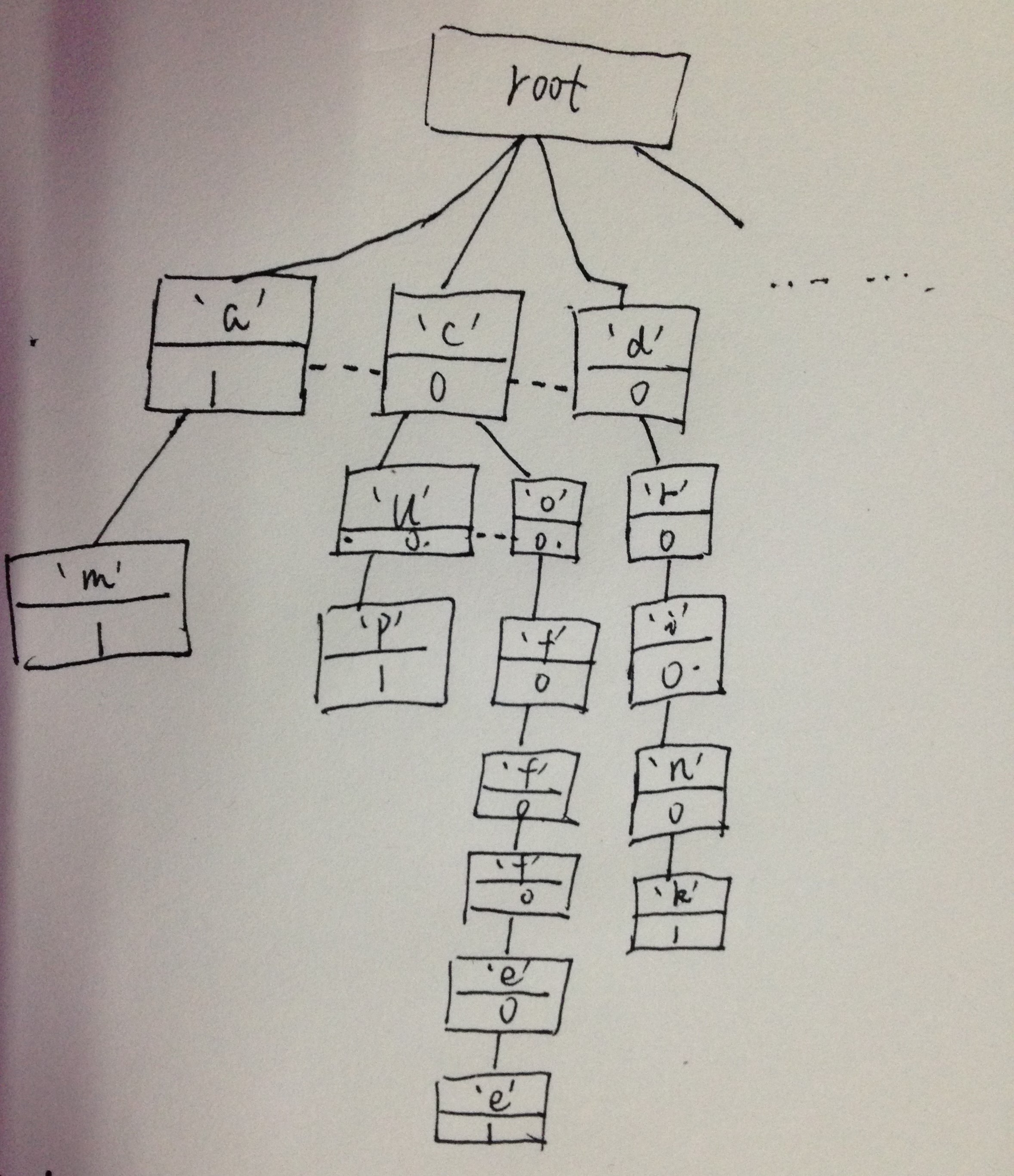
（實線表示next指標，虛線表示sib指標）
從圖中的字典樹可以看到，a這個單詞出現1次，am出現了1次，cup出現了1次，coffee出現了1次，drink出現了1次等等。
那麼，根據這個資料結構，在通篇掃描完文章之後，就可以建立起該Trie樹。之後遍歷這棵樹就可以得到文章中出現單詞的次數。而這棵樹，實際上是一顆26叉樹。

Q：給出10億個無序的32位整型數，求出它們的中位數。

A：這是筆試裡的最後一題，我自己想了一個辦法，但在筆試時沒細想，只給出了思路。
建立1000個數組（分別標識為-500, -499…1, 2, 3, 4…499）——這樣標識是有原因的，至於為什麼要這樣標識，下文會講到。
確保-499陣列中的數大於-500陣列中的數，-498陣列中的數大於-499陣列中的數等等，以此類推。
接下來，就要將這10億個無序32位整數劃分到這1000個數組中了，劃分的方法我也想好了，這很關鍵。

1. 首先，設定一個常數等於const int cst = int32_MAX（32位整數的最大值） / 500。
2. 遍歷給定的10億個數，每個數設為a
   i，讓ai除以cst，得出一個標準值std（整型）。
3. std就會是[-500, 500)中的其中一個數，那麼這個std等價於對映到1000個數組中的其中一個數組的標識，所以ai就可以通過這個std，塞入對應的陣列中。
4. 遍歷過後，10億個數就可以劃分到這1000個數組中。

那麼，這1000個數組由小到大排列，陣列的大小可知，那麼就可以知道中位數處於哪個陣列中。
接下來將中位數所處的陣列獨立處理，設計一個閾值α（假定為50），如果該陣列的大小小於該閾值，就排序，取出中位數即可。
大於閾值，重複上述劃分法（當然了，當陣列的大小過小時，可以減小劃分組數）。
這就是我對這個題目的解法，讀者們如果發現有不對的地方希望指正，有更好的辦法希望可以點撥一下我。

一面：

Q：給出一個連連看的演算法

連連看的規則很簡單，其實就是給定兩個點，尋找兩點之間是否有通路——這是我一開始的看法。然後按照我的這個判斷，我給出了一個由兩點中的一點出發的深度優先遍歷（DFS）的辦法，並且已經走過的區域不準再走，這樣子時間複雜度應該是O（n*m）[假定連連看矩陣有n*m大]。
面試官聽了我這個辦法之後，給我了一個提示——連連看中兩個相同圖示中的連線只能拐兩次。

聽了這句話後，我沒想到這是個提示= =，直接就說遍歷的時候做個判斷就好了。但其實我錯了，後面面試官跟我說了一個十分高效的演算法，就是依賴於這個規則的。

下面來說說這個巧妙的演算法：
先給出個示意圖：

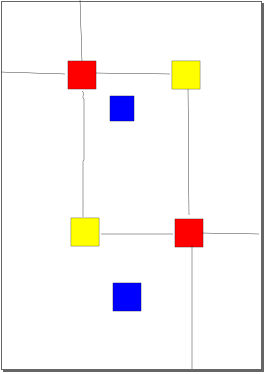
圖中，兩個紅點就是兩個需要連通的點，然後將紅點上下左右可以連通到的最遠的點都標記起來（如圖灰色線就是所有需要標記的點的路徑），由於有隻能拐兩次這個設定，所以假如其中一個紅點的灰色線中的某點能作一條直線到對方紅點的灰色線上的某一個點，就證明可以連通，遍歷完所有灰色的點都找不到合適的路徑，則證明不能連通。

這個方法，巧妙地利用了拐兩次以內這個規則，效率上要比DFS快得多。

Q:段式記憶體管理和頁式記憶體管理的區別

A:

• 段式記憶體管理：系統可以給一個應用程式分配很多的段來進行記憶體管理，但是每一段的大小是不同的，然而每一段都具有邏輯意義——比如程式碼段、共享資料段等。每一段程式都可以獨立編制。而段的內容通過邏輯地址來訪問——[段號：段內偏移量]。
• 頁式記憶體管理：系統可以給一個應用程式分配很多的頁來進行記憶體管理，每頁的大小是確定的。通過建立虛擬地址和實體記憶體地址的一 一對應頁表來訪問每一頁的內容。
• 現在的機器都很少單獨使用段式記憶體管理或者頁式記憶體管理，基本都使用上述兩者的合成品——段頁式記憶體管理。

二面：

Q：給定一個nxm的迷宮，中間有很多阻礙，求從(0,0)走到(n,m)的最短路徑。

A:這個我給出的解法是深度優先搜尋，然而面試官好像沒聽懂。。。＝ ＝

Q：n級臺階，你一次可以選擇走一步或者兩步，統計能走到第n級臺階的走法數。

A:這題不難，我直接給出程式碼好了。

int num = 0;
void count(int n, int now) {
    if (now >= n) {
        if (now == n) num++;
        return;
    }
    count(n, now + 1);
    count(n, now + 2);
}

int main() {
    count(n, 0);
    cout<<"總共有"<<num<<"種走法"<<endl;
    return 0;
}

還有一種解法就是，兩步在所有走法中只可能出現0 - n/2次，然後出現0次，出現1次，出現2次……每種情況都可以再運用排列組合公式求得走法數，最後加起來就可以得到總和。

Q：求字串長度

A：這題，我給了個很一般的演算法，就是一個while迴圈統計字元，遇到\n就停。
但是其實最好的辦法是：

unsigned long len(char *str) {
    return sizeof(str) / sizeof(char);
}

=.=崩盤

Q：判斷一個數是不是2的n次方

A：我自己想了一個時間複雜度為O(log(n))的辦法，這個辦法就是：
設一個初始數為2，不斷對它進行平方操作，那它就以2, 4, 16, 256…的速度指數性增長。設判斷數為514，那麼這個演算法是這麼操作的，發現了514處於2^8~2^16之間，那麼接下來在2^8 x 2^8這步平方操作中，對另一半2^8進行和上面類似的操作，就是按[2, 2^2, 2^4, 2^8),這樣的方式增長，不斷的和2^8乘在一起，再找到514處於2^9~2^10之間，然而9跟10只有1的差距，而514!=2^9且514！=2^10，所以514不是2的n次方。

不知道我有沒有講清楚，要是看不懂可以在評論問我。

後來我上網查了一下，發現了一個更為快捷的方法，時間複雜度是常數。附上程式碼：

bool isPower2(int num){
    if (num <= 0) return false;
    if (num == 1) return true;
    return (num & (num - 1)) == 0;
}