點到鏈的距離

設點 $k$，鏈的端點 $(i,j)$

定義 $d[i,j$

可得 $D$

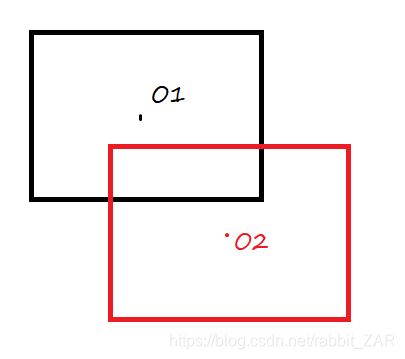
原理如圖：

矩形的相交區域座標

設黑色矩形左上角座標 ( x1 , y1 )，右下角 ( x2 , y2 ) ;

紅矩形左上角座標 ( a1 , b1 )，右下角 ( a2 , b2 )。

根據重點公式，可以算出 $O1 = ( \frac{ x1 + x2 }{2} , \frac{ y1 + y2 }{2} ) ，O2 = ( \frac{ a1 + a2 }{2} , \frac{ b1 + b2 }{2})$。

所以相交的條件就是：

$abs(\frac{ x1 + x2 }{2}-\frac{ a1 + a2 }{2})<=\frac{x2-x1}{2}+\frac{a2-a1}{2}$

且

$abs(\frac{ y1 + y2 }{2}-\frac{ b1 + b2 }{2})<=\frac{y2-y1}{2}+\frac{b2-b1}{2}$

整理得

$abs( x1 + x2 - a1 - a2)<=x2-x1+a2-a1$

且

$abs( y1 + y2 - b1 - b2)<=y2-y1+b2-b1$

判斷完相交，就是求相交部分的座標了。

也很好看出來，左上角是 $( max(x1,a1) , min(x2,a2))$，右下角是 $(max(y1,b1),min(y2,b2))$。

假的範圍？

對於一些大得詭異的資料範圍，可以先計算下是不是真的需要處理這麼大的範圍。

有時候資料大到一定程度可以直接輸出不用考慮。