稀疏矩陣

一、稀疏矩陣的定義

      對於那些零元素數目遠遠多於非零元素數目，並且非零元素的分佈沒有規律的矩陣稱為稀疏矩陣（sparse）。

      人們無法給出稀疏矩陣的確切定義，一般都只是憑個人的直覺來理解這個概念，即矩陣中非零元素的個數遠遠小於矩陣元素的總數，並且非零元素沒有分佈規律。

二、稀疏矩陣的壓縮儲存

      由於稀疏矩陣中非零元素較少，零元素較多，因此可以採用只儲存非零元素的方法來進行壓縮儲存。

      由於非零元素分佈沒有任何規律，所以在進行壓縮儲存的時侯需要儲存非零元素值的同時還要儲存非零元素在矩陣中的位置，即非零元素所在的行號和列號，也就是在儲存某個元素比如a_ij的值的同時，還需要儲存該元素所在的行號i和它的列號j，這樣就構成了一個三元組(i,j,a_ij

      三元組可以採用順序表示方法，也可以採用鏈式表示方法，這樣就產生了對稀疏矩陣的不同壓縮儲存方式。

a、稀疏矩陣的順序實現

      若把稀疏矩陣的三元組線性表按順序儲存結構儲存，則稱為稀疏矩陣的三元組順序表。

      順序表中除了儲存三元組外，還應該儲存矩陣行數、列數和總的非零元素數目，這樣才能唯一的確定一個矩陣。

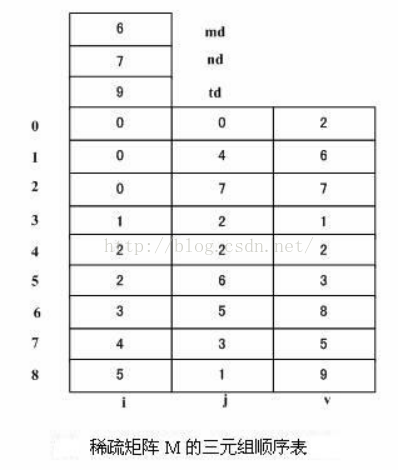
　　順序儲存結構儲存三元組線性表的C#程式碼如下：

    struct tupletype<T>
    {
        public int i;//行號
        public int j;//列號
        public T v; //元素值
        public tupletype(int i, int j, T v)
        {
            this.i = i;
            this.j = j;
            this.v = v;
        }
    }
    class spmatrix<T>
    {
        int MAXNUM;//非零元素的最大個數
        int md;//行數值
        int nd;//列數值
        int td;//非零元素的實際個數
        tupletype<T>[] data;//儲存非零元素的值及一個表示矩陣行數、列數和總的非零元素數目的特殊三元組
    }
 

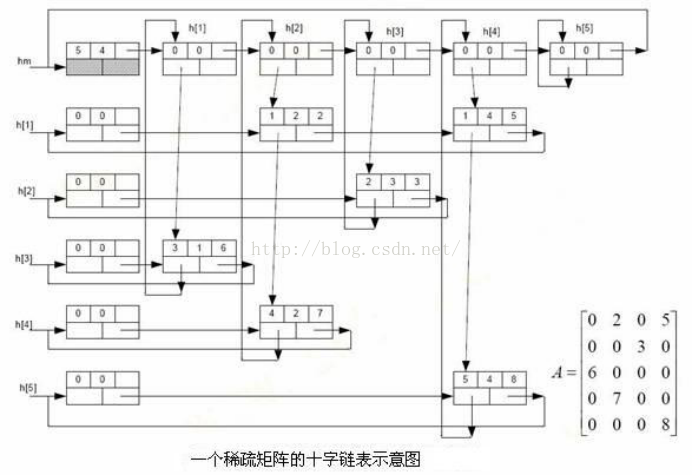
b、稀疏矩陣的十字連結串列實現

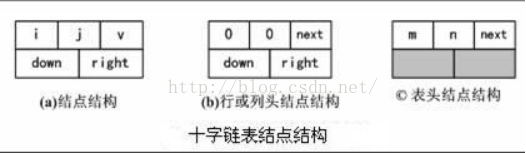
      十字連結串列結點分為三類 :

      表結點，它由五個域組成，其中i和j儲存的是結點所在的行和列，right和down儲存的是指向十字連結串列中該結點所有行和列的下一個結點的指標，v用於存放元素值。

      行頭和列頭結點，這類結點也有域組成，其中行和列的值均為零，沒有實際意義，right和down的域用於在行方向和列方向上指向表結點，next用於指向下一個行或列的表頭結點。

      總表頭結點，這類結點與表頭結點的結構和形式一樣，只是它的i和j存放的是矩陣的行和列數。

十字連結串列可以看作是由各個行連結串列和列連結串列共同搭建起來的一個綜合連結串列，每個結點aij既是處在第i行連結串列的一個結點，同時也是處在第j列連結串列上的一個結點，就你是處在十字交叉路口上的一個結點一樣，這就是十字連結串列的由來。

十字連結串列中的每一行和每一列連結串列都是一個迴圈連結串列，都有一個表頭結點。

三、稀疏矩陣的實現

      矩陣運算通常包括矩陣轉置、矩陣加、矩陣乘、矩陣求逆等。這裡僅討論最簡單的矩陣轉置運算演算法。

      矩陣轉置運算是矩陣運算中最重要的一項，它是將m×n的矩陣變成另外一個n×m的矩陣，使原來矩陣中元素的行和列的位置互換而值保持不變，即若矩陣N是矩陣M的轉置矩陣，則有：M[i][j]=N[j][i] (0≤i≤m-1,0≤j≤n-1)。

      三元組表表示轉置矩陣的具體方法是：

      第一步：根據M矩陣的行數、列數和非零元總數確定N矩陣的列數、行數和非零元總數。

      第二步：當三元組表非空（M矩陣的非零元不為0）時，對M中的每一列col(0≤col≤n-1)，通過從頭至尾掃描三元組表data，找出所有列號等於col的那些三元組，將它們的行號和列號互換後依次放人N的data中，即可得到N的按行優先的壓縮存貯表示。

  class spmatrix<T>
    {
        int MAXNUM;//非零元素的最大個數
        int md;//行數值
        int nd;//列數值
        int td;//非零元素的實際個數
        tupletype<T>[] data;//儲存非零元素的值及一個表示矩陣行數、列數和總的非零元素數目的特殊三元組
        public int Md
        {
            get
            {
                return md;
            }
            set
            {
                md = value;
            }
        }
        public int Nd
        {
            get
            {
                return nd;
            }
            set
            {
                nd = value;
            }
        }
        public int Td
        {
            get
            {
                return td;
            }
            set
            {
                td = value;
            }
        }
        //三元組表的data屬性
        public tupletype<T>[] Data
        {
            get
            {
                return data;
            }
            set
            {
                data = value;
            }
        }
        //初始化三元組順序表
        public spmatrix() { }
        public spmatrix(int maxnum, int md, int nd)
        {
            this.MAXNUM = maxnum;
            this.md = md;
            this.nd = nd;
            data = new tupletype<T>[MAXNUM];
        }
        //設定三元組表元素的值
        public void setData(int i, int j, T v)
        {
            data[td] = new tupletype<T>(i, j, v);
            td++;
        }
        //矩陣轉置演算法
        public spmatrix<T> Transpose()
        {
            spmatrix<T> N = new spmatrix<T>();
            int p, q, col;
            N.MAXNUM = MAXNUM;
            N.nd = md;
            N.md = nd;
            N.td = td;
            N.data = new tupletype<T>[N.td];
            if (td != 0)
            {
                q = 0;//控制轉置矩陣的下標
                for (col = 0; col < nd; col++)//掃描矩陣的列
                {
                    for (p = 0; p < td; p++)//p控制被轉置矩陣的下標
                    {
                        if (data[p].j == col)
                        {
                            N.data[q].i = data[p].j;
                            N.data[q].j = data[p].i;
                            N.data[q].v = data[p].v;
                            q++;
                        }
                    }
                }
            }
            return N;
        }

美文美圖