讓我們從頭說起，首先AUC是一種用來度量分類模型好壞的一個標準。這樣的標準其實有很多，例如：大約10年前在machine learning文獻中一統天下的標準：分類精度；在資訊檢索(IR)領域中常用的recall和precision，等等。其實，度量反應了人們對” 好”的分類結果的追求，同一時期的不同的度量反映了人們對什麼是”好”這個最根本問題的不同認識，而不同時期流行的度量則反映了人們認識事物的深度的變 化。近年來，隨著machine learning的相關技術從實驗室走向實際應用，一些實際的問題對度量標準提出了新的需求。特別的，現實中樣本在不同類別上的不均衡分佈(class distribution imbalance problem)。使得accuracy這樣的傳統的度量標準不能恰當的反應分類器的performance。舉個例子：測試樣本中有A類樣本90個，B 類樣本10個。分類器C1把所有的測試樣本都分成了A類，分類器C2把A類的90個樣本分對了70個，B類的10個樣本分對了5個。則C1的分類精度為 90%，C2的分類精度為75%。但是，顯然C2更有用些。另外，在一些分類問題中犯不同的錯誤代價是不同的(cost sensitive learning)。這樣，預設0.5為分類閾值的傳統做法也顯得不恰當了。

為了解決上述問題，人們從醫療分析領域引入了一種新的分類模型performance評判方法——ROC分析。ROC分析本身就是一個很豐富的內容，有興趣的讀者可以自行Google。由於我自己對ROC分析的內容瞭解還不深刻，所以這裡只做些簡單的概念性的介紹。

ROC的全名叫做Receiver Operating Characteristic，其主要分析工具是一個畫在二維平面上的曲線——ROC curve。平面的橫座標是false positive rate(FPR)，縱座標是true positive rate(TPR)。對某個分類器而言，我們可以根據其在測試樣本上的表現得到一個TPR和FPR點對。這樣，此分類器就可以對映成ROC平面上的一個點。調整這個分類器分類時候使用的閾值，我們就可以得到一個經過(0, 0)，(1, 1)的曲線，這就是此分類器的ROC曲線。一般情況下，這個曲線都應該處於(0, 0)和(1, 1)連線的上方。因為(0, 0)和(1, 1)連線形成的ROC曲線實際上代表的是一個隨機分類器。如果很不幸，你得到一個位於此直線下方的分類器的話，一個直觀的補救辦法就是把所有的預測結果反向，即：分類器輸出結果為正類，則最終分類的結果為負類，反之，則為正類。雖然，用ROC curve來表示分類器的performance很直觀好用。可是，人們總是希望能有一個數值來標誌分類器的好壞。於是Area Under roc Curve(AUC)就出現了。顧名思義，AUC的值就是處於ROC curve下方的那部分面積的大小。通常，AUC的值介於0.5到1.0之間，較大的AUC代表了較好的performance。好了，到此為止，所有的 前續介紹部分結束，下面進入本篇帖子的主題：AUC的計算方法總結。

最直觀的，根據AUC這個名稱，我們知道，計算出ROC曲線下面的面積，就是AUC的值。事實上，這也是在早期Machine Learning文獻中常見的AUC計算方法。由於我們的測試樣本是有限的。我們得到的AUC曲線必然是一個階梯狀的。因此，計算的AUC也就是這些階梯下面的面積之和。這樣，我們先把score排序(假設score越大，此樣本屬於正類的概率越大)，然後一邊掃描就可以得到我們想要的AUC。但是，這麼 做有個缺點，就是當多個測試樣本的score相等的時候，我們調整一下閾值，得到的不是曲線一個階梯往上或者往右的延展，而是斜著向上形成一個梯形。此時，我們就需要計算這個梯形的面積。由此，我們可以看到，用這種方法計算AUC實際上是比較麻煩的。

一個關於AUC的很有趣的性質是，它和Wilcoxon-Mann-Witney Test是等價的。這個等價關係的證明留在下篇帖子中給出。而Wilcoxon-Mann-Witney Test就是測試任意給一個正類樣本和一個負類樣本，正類樣本的score有多大的概率大於負類樣本的score。有了這個定義，我們就得到了另外一中計算AUC的辦法：得到這個概率。我們知道，在有限樣本中我們常用的得到概率的辦法就是通過頻率來估計之。這種估計隨著樣本規模的擴大而逐漸逼近真實值。這 和上面的方法中，樣本數越多，計算的AUC越準確類似，也和計算積分的時候，小區間劃分的越細，計算的越準確是同樣的道理。具體來說就是統計一下所有的 M×N(M為正類樣本的數目，N為負類樣本的數目)個正負樣本對中，有多少個組中的正樣本的score大於負樣本的score。當二元組中正負樣本的 score相等的時候，按照0.5計算。然後除以MN。實現這個方法的複雜度為O(n^2)。n為樣本數（即n=M+N）

第三種方法實際上和上述第二種方法是一樣的，但是複雜度減小了。它也是首先對score從大到小排序，然後令最大score對應的sample 的rank為n，第二大score對應sample的rank為n-1，以此類推。然後把所有的正類樣本的rank相加，再減去正類樣本的score為最 小的那M個值的情況。得到的就是所有的樣本中有多少對正類樣本的score大於負類樣本的score。然後再除以M×N。即

AUC=((所有的正例位置相加)-M*(M+1))/(M*N)

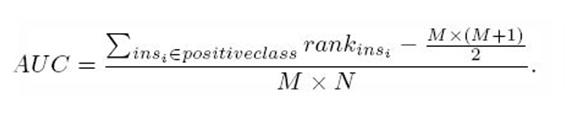
另外，特別需要注意的是，再存在score相等的情況時，對相等score的樣本，需要 賦予相同的rank(無論這個相等的score是出現在同類樣本還是不同類的樣本之間，都需要這樣處理)。具體操作就是再把所有這些score相等的樣本 的rank取平均。然後再使用上述公式。