總結:Bias(偏差),Error(誤差),Variance(方差)及CV(交叉驗證)
前言
此片有很多別人的東西,直接搬過來了,都有註釋,裡面也有一些自己的理解和需要注意的地方,以此記錄一下,總結如下,思想不夠成熟,以後再補充,如有錯誤請不吝指正
犀利的開頭
在機器學習中,我們用訓練資料集去訓練(學習)一個model(模型),通常的做法是定義一個Loss function(誤差函式),通過將這個Loss(或者叫error)的最小化過程,來提高模型的效能(performance)。然而我們學習一個模型的目的是為了解決實際的問題(或者說是訓練資料集這個領域(field)中的一般化問題),單純地將訓練資料集的loss最小化,並不能保證在解決更一般的問題時模型仍然是最優,甚至不能保證模型是可用的。這個訓練資料集的loss與一般化的資料集的loss之間的差異就叫做generalization error=bias+variance。
Error = Bias^2 + Variance+Noise
- 什麼是Bias(偏差)
Bias反映的是模型在樣本上的輸出與真實值之間的誤差,即模型本身的精準度,即演算法本身的擬合能力
- 什麼是Variance(方差)
Variance反映的是模型每一次輸出結果與模型輸出期望之間的誤差,即模型的穩定性。反應預測的波動情況。
- 什麼是Noise(噪聲)
這就簡單了,就不是你想要的真正資料,你可以想象為來破壞你實驗的元凶和造成你可能過擬合的原因之一,至於為什麼是過擬合的原因,因為模型過度追求Low Bias會導致訓練過度,對測試集判斷表現優秀,導致噪聲點也被擬合進去了
簡單的例子理解Bias和Variance
- 開槍問題
想象你開著一架黑鷹直升機,得到命令攻擊地面上一隻敵軍部隊,於是你連打數十梭子,結果有一下幾種情況:
1.子彈基本上都打在隊伍經過的一棵樹上了,連在那棵樹旁邊等兔子的人都毫髮無損,這就是方差小(子彈打得很集中),偏差大(跟目的相距甚遠)。
2.子彈打在了樹上,石頭上,樹旁邊等兔子的人身上,花花草草也都中彈,但是敵軍安然無恙,這就是方差大(子彈到處都是),偏差大(同1)。
3.子彈打死了一部分敵軍,但是也打偏了些打到花花草草了,這就是方差大(子彈不集中),偏差小(已經在目標周圍了)。
4.子彈一顆沒浪費,每一顆都打死一個敵軍,跟抗戰劇裡的八路軍一樣,這就是方差小(子彈全部都集中在一個位置),偏差小(子彈集中的位置正是它應該射向的位置)。
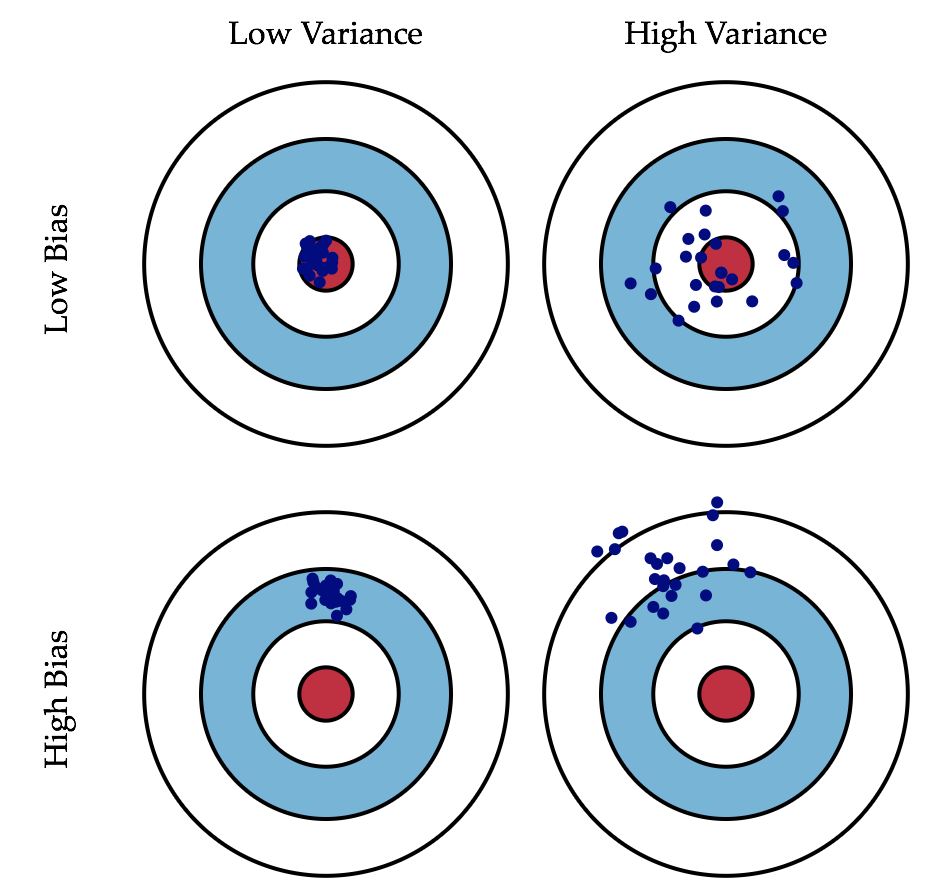
-再來個射箭問題:假設你在射箭,紅星是你的目標,以下是你的射箭結果
分析:
我們可以看到,在Low Variance的一列,資料分佈是非常集中的,恩,小夥子,你的穩定性很好,方差很小,表現的很聚集。而第二列就是High Variance的一列,機智的你可能一下就看出來了,沒錯,飄來飄去的,非常不穩定!
看下Low Bias這一行,命中紅心的次數很多對不對,說明你還是有準頭的,至少偏差不算大,我要是裁判,我就不管你沒射中幾隻箭飄到哪去了(方差大,不集中),畢竟我看的是命中了多少(準確度),而High Bias這一行,明顯可以看出一支箭都沒射中,表現很差,偏離目標好遠,負分滾粗!
綜合起來看,我們需要的模型最好是兩個L,又準確又穩定,妥妥的,但是,這個在現實模型中是不會存在的。你只能權衡著來
Bias,Variance和Overfitting(過擬合),Underfitting(欠擬合)
過擬合,也就是我對訓練樣本能夠百分百命中了,超級擬合了,但是測試時候就掉鏈子,擬合很差,也就是我們說的泛化效能不好的問題,所以如果太追求在訓練集上的完美而採用一個很複雜的模型,會使得模型把訓練集裡面的噪聲都當成了真實的資料分佈特徵,從而得到錯誤的資料分佈估計。
一句話,過擬合會出現高方差問題
欠擬合:訓練樣本太少,導致模型就不足以刻畫資料分佈了,體現為連在訓練集上的錯誤率都很高的現象。
一句話,欠擬合會出現高偏差問題
怎麼避免過擬合和欠擬合
避免欠擬合(刻畫不夠)
- 尋找更好的特徵—–具有代表性的
- 用更多的特徵—–增大輸入向量的維度
避免過擬合(刻畫太細,泛化太差)
- 增大資料集合—–使用更多的資料,噪聲點比重減少
- 減少資料特徵—–減小資料維度,高維空間密度小
- 正則化方法—–即在對模型的目標函式(objective function)或代價函式(cost function)加上正則項
為什麼要用交叉驗證(Cross-Validation)
1.交叉驗證,這是僅使用訓練集衡量模型效能的一個方便技術,不用建模最後才使用測試集
2.Cross-validation 是為了有效的估測 generalization error(泛化誤差) 所設計的實驗方法,而generalization error=bias+variance
首先:bias和variance分別從兩個方面來描述了我們學習到的模型與真實模型之間的差距。Bias是 “用所有可能的訓練資料集訓練出的所有模型的輸出的平均值” 與 “真實模型”的輸出值之間的差異;Variance則是“不同的訓練資料集訓練出的模型”的輸出值之間的差異。
可以發現,怎麼來平衡Bias和Variance則成了我們最大的任務了,也就是怎麼合理的評估自己模型呢?我們由此提出了交叉驗證的思想,以K-fold Cross Validation(記為K-CV)為例,基本思想如下:(其他更多方法請看@bigdataage –交叉驗證(Cross-Validation))
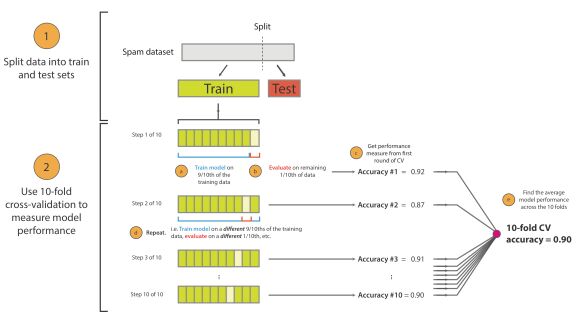
將原始資料分成K組(一般是均分),將每個子集資料分別做一次驗證集,其餘的K-1組子集資料作為訓練集,這樣會得到K個模型,用這K個模型最終的驗證集的分類準確率的平均數作為此K-CV下分類器的效能指標.K一般大於等於2,實際操作時一般從3開始取,只有在原始資料集合資料量小的時候才會嘗試取2. 而K-CV 的實驗共需要建立 k 個models,並計算 k 次 test sets 的平均辨識率。在實作上,k 要夠大才能使各回合中的 訓練樣本數夠多,一般而言 k=10 (作為一個經驗引數)算是相當足夠了。
看不清上面的就來一幅更簡單的
每次的training_set 紅色, validation_set白色 ,也就是說k=5的情況了
注意:交叉驗證使用的僅僅是訓練集!!根本沒測試集什麼事!很多部落格都在誤導!
這也就解決了上面剛開始說的Variance(不同訓練集產生的差異),Bias(所有data訓練結果的平均值)這兩大問題了!因為交叉驗證思想集合了這兩大痛點,能夠更好的評估模型好壞!
說白了,就是你需要用下交叉驗證去試下你的演算法是否精度夠好,夠穩定!你不能說你在某個資料集上表現好就可以,你做的模型是要放在整個資料集上來看的!畢竟泛化能力才是機器學習解決的核心
Bias、Variance和K-fold的關係
下面解釋一下Bias、Variance和k-fold的關係:k-fold交叉驗證常用來確定不同型別的模型(線性、指數等)哪一種更好,為了減少資料劃分對模型評價的影響,最終選出來的模型型別(線性、指數等)是k次建模的誤差平均值最小的模型。當k較大時,經過更多次數的平均可以學習得到更符合真實資料分佈的模型,Bias就小了,但是這樣一來模型就更加擬合訓練資料集,再去測試集上預測的時候預測誤差的期望值就變大了,從而Variance就大了;反之,k較小時模型不會過度擬合訓練資料,從而Bias較大,但是正因為沒有過度擬合訓練資料,Variance也較小。