ML:Scikit-Learn 學習筆記(3) --- Nearest Neighbors 最近鄰 迴歸及相關演算法
1 最近鄰迴歸
最近鄰迴歸是用在標籤值是連續取值的場景智商的,而不是離散取值,而是用最近鄰迴歸進行查詢的點,最後得到的結果是其所有最近鄰居的平均值。
scikit-learn 在迴歸部分,同樣實現了兩種迴歸演算法,和之前的一樣,和KNN思想近似的KNeighborsRegressor ,和RNN思想近似的RadiusNeighborsRegressor 。其中KNR依然是使用K個最相近的點,RNR使用半徑r範圍內的點,他們倆的具體引數都可以由使用者指定。
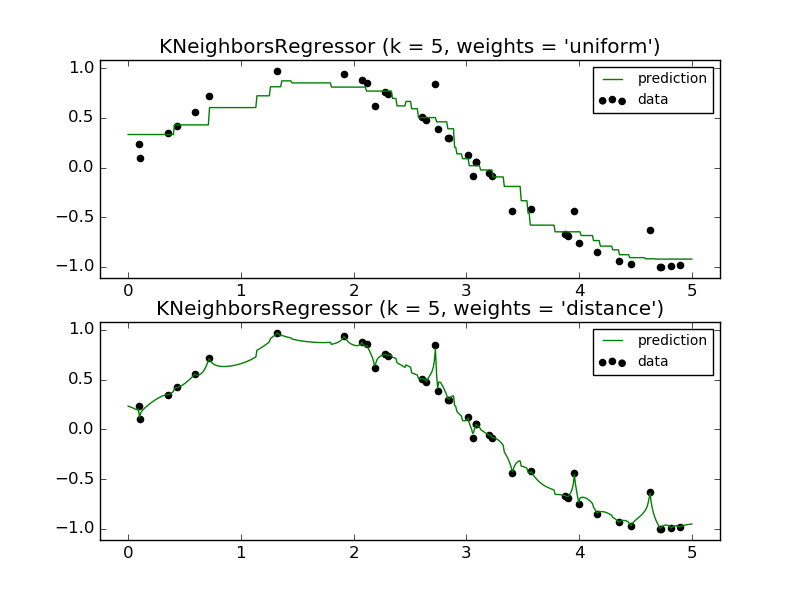
最原始的最近鄰迴歸演算法,在考慮每一個鄰居點時,都給與他相同的權重。不過和最近鄰分類一樣的是,在很多情況下,如果給距離近的點更高的權重,那麼效果會更加不錯。在Scikit-learn當中,可以使用weight這個引數來指定(uniform或distance,可以參考上一章的內容)。下圖就是這兩種取值的一個示例
scikit-learn對於最近鄰迴歸,給了一個例子,即給定上一半的人臉,推測其下一半的人臉

感興趣的小夥伴可以到這裡檢視人臉推測示例
2 最近鄰搜尋相關演算法
1 Brute Force
在根據官方文件介紹之前,首先貼一個來自於百度百科的介紹:
BF(Brute
Force)演算法是普通的模式匹配演算法,BF演算法的思想就是將目標串S的第一個字元與模式串T的第一個字元進行匹配,若相等,則繼續比較S的第二個字元和
T的第二個字元;若不相等,則比較S的第二個字元和T的第一個字元,依次比較下去,直到得出最後的匹配結果。BF演算法是一種蠻力演算法。
好了,這裡介紹的最近鄰演算法是什麼意思?不是已經介紹了KNN RNN等了麼?
恩,這裡的演算法是指如何搜尋最近鄰局,要知道最近鄰的演算法每次都需要在所有取值點當中進行搜尋,因此有合適的演算法去加速這個過程是很有必要的。
Brute Force 演算法就是一個最原始(蠻力)鄰居搜尋做法,Brute Force在尋找鄰居時,會把輸入的點同所有樣本中的點做一個距離計算,然後再排序選擇最近的點。因此,對於一個有N個D維樣本的情況下,這個做法的時間複雜度是O[D N^2].正因如此,這個演算法只適合用在一些樣本容量不太大的場景當中,但是在真正的機器學習場景中,往往樣本量也會很大吧,這時候BF也不那麼使用。
如果你想在scikit-learn當中使用這個演算法,可以設定關鍵詞algorithm為‘brute’就可以了,計算的細節可以參照sklearn.metrics.pairwise.
2 KD-Tree
KD-Tree 也就是我們熟知的KD樹,也是一個很適合用來搜尋最近鄰的做法。為了解決BF演算法效率低下的問題,人們提出了很多樹形結構的演算法,樹形結構的主要貢獻在於,它們一般通過事先的合理組織,降低了我們搜尋中的開銷,也就是使用樹形結構的演算法,我們在搜尋時可以不用每個樣本都去計算距離了,這無疑降低了很多的開銷。
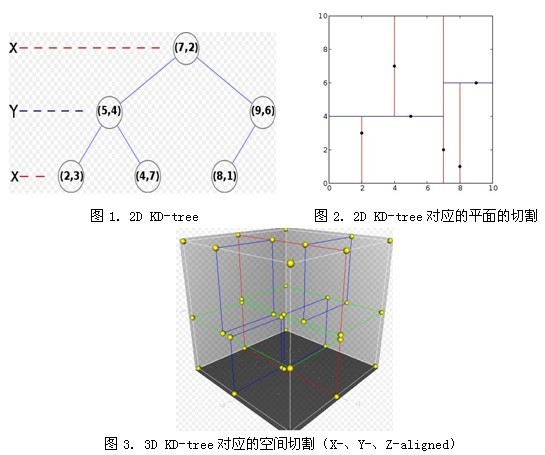
我這裡有一個資料,可幫助大家理解KD-樹,因為我單單貼出解釋,估計大家也不懂
KD樹核心思想簡介
如果我們知道一個點A,他和B的距離很遠,而B的距離又和C很近,那麼我們也可以推出A和C的距離很遠,那麼我們就不用去考慮他們之間的距離了。基於這一類的演算法,搜尋的時間複雜度可以下降到O[D N \log(N)] 或者更好,這樣我們就可以拋棄那效率低下的BF演算法了。
而KD樹,則是最早被廣泛用於代替BF進行搜尋的演算法,並且KD樹是一個比四叉樹(2維)和八叉樹(3維)更加抽象的K維樹。KD樹使用了二叉樹作為基本結構,他用遞迴的方式對資料進行劃分(每一層進行一個維度的劃分)。KD樹的構建過程是十分迅速的,因為他只需要根據座標軸進行劃分,不用計算多維度的距離。而且只要KD樹建立起來,對於每一個點的搜尋,其時間複雜度都只有O[\log(N)] 了。在不太高的維度(小於20)下,KD樹的效果是很不錯的,不過當維度走向更高時,KD樹的效率也會隨之下降,這也呼應了我們之前提到的“維度之殤”的問題。
在scikit-learn當中,如果需要使用這個演算法,設定algorithm為‘kd_tree’就可以了,具體的計算程式碼可以參照KDTree裡的程式碼。
3 Ball-Tree
Ball-Tree的資料比較少,特別是中文的,這個我之前也沒有接觸到,這裡留一個Wiki的連線Ball tree
好了,KD-Tree是為了解決Brute Force的效率問題,那麼Ball-Tree也就是為了解決KD-Tree在高維情況下的效率不佳的另一個做法了。KD樹是在笛卡爾座標系中進行資料劃分的,而Ball樹則是在 nesting hyper-spheres當中(大概是網狀超球面下,我也不大好翻譯)劃分的。Ball樹在構建的時候,比起KD樹要複雜許多,不過在最後的搜尋過程中,其表現就會非常好。
Ball樹根據質心(或者理解為圓心,原詞 centroid 質心,但我看他的描述 很像圓心,等我查明瞭,再更新)C和半徑r對資料進行遞迴的劃分,每一個數據點都會被劃分到一個特定的圓心C和半徑r的的超球體裡面,在搜尋的時候,候選的點會使用如下的不等式進行篩選:
|x+y| <= |x| + |y|
通過這樣的篩選,只用根據半徑和圓心就可以計算出一個球體裡包含點的距離的上界和下界,那麼這樣就可以減少很多的減少很多點的計算了。一個超球體裡面包含的點,距離其質心都是有一定的距離範圍的,那麼對於這一個球體裡的所有值,我們只需要首先計算和質心的距離,就可以(根據上下界)判定我們是否需要進一步的搜尋了。
在scikit-learn當中,如果要使用Ball樹,可以algorithm = ‘ball_tree’的設定,相關程式碼在sklearn.neighbors.BallTree裡
恩,下一章裡我們談談這些演算法的具體選擇策略好了。
附錄