資料分析之 – 離群值（Outliers）

一：什麼是Outliers

Outliers是統計學專業術語，是指相比一組資料中的其它資料的極限值

二：極限值意味什麼

 1. 決定哪些值是Outliers是一個主觀行為，有一些基準資料來決定是否一個值是一個Outliers，這些基準是任意選擇的，比如P<=0.5就是一個任意選擇的基準

2. 一個基準是用BoxPlot來決定適度離群值（mild Outliers）和極限離群值（extreme Outliers），適度離群值是任何值1.5倍大於基於剩下所有的值的IQR，極限離群值是任何值3倍大於剩下所有的值的IQR，IQR（Interquartile Range

三：使用Box Plot來發現Outliers

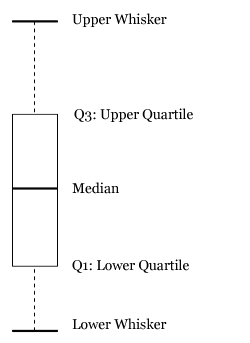
一個典型的Box Plot是基於以下五個值計算而來的

a. 一組樣本的最小值

b. 一組樣本的最大值

c. 一組樣本的中值

d. 下四分位數（Lower Quartile / Q1）

e. 上四分位數（Upper Quartile / Q3）

根據這五個值構建出來基本的Box Plot，某些圖形軟體還會顯示平均值，IQR= Q3 – Q1

顯然超出上下四分位數的值可以看做為Outliers。我們通過眼睛就可以很好的觀察到這些Outliers

一個顯示適度和極限Outliers值的Box plot顯示如下：

四：示例說明及JfreeChart的實現

假設一組資料為：2,4,6,8,12,14,16,18,20,25,45

中值 Median = 14

Q1-下四分位數（11 * 0.25 = 3） = 7

Q3-上四分位數（11 * 0.75 = 9） =19

IQR（Q3 – Q1） = 12

1.5 * IQR = 18

最小值（6 – 1.5 * IQR）= 2

最大值（20 + 1.5 * IQR）= 25

很顯然值45是一個適度Outliers

對比的一組資料為：2,4,6,8,12,14,16,18,20,25,26

從圖上可以看出Series0的資料存在Outliers，一個紅色三角形已經表明

同樣Series1的資料是一組非常好的資料，沒有Outliers.

下面是Java原始碼：

package com.dataanalysis.plots; import java.awt.Font; import java.util.ArrayList; import java.util.List; import org.jfree.chart.ChartPanel; import org.jfree.chart.JFreeChart; import org.jfree.chart.axis.CategoryAxis; import org.jfree.chart.axis.NumberAxis; import org.jfree.chart.labels.BoxAndWhiskerToolTipGenerator; import org.jfree.chart.plot.CategoryPlot; import org.jfree.chart.renderer.category.BoxAndWhiskerRenderer; import org.jfree.data.statistics.BoxAndWhiskerCategoryDataset; import org.jfree.data.statistics.DefaultBoxAndWhiskerCategoryDataset; import org.jfree.ui.ApplicationFrame; import org.jfree.ui.RefineryUtilities; public class BoxAndWhiskerDemo extends ApplicationFrame { /** * */ private static final long serialVersionUID = -3205574763811416266L; /** * Creates a new demo. * * @param title the frame title. */ public BoxAndWhiskerDemo(final String title) { super(title); final BoxAndWhiskerCategoryDataset dataset = createSampleDataset(); final CategoryAxis xAxis = new CategoryAxis("Type"); final NumberAxis yAxis = new NumberAxis("Value"); yAxis.setAutoRangeIncludesZero(false); final BoxAndWhiskerRenderer renderer = new BoxAndWhiskerRenderer(); renderer.setFillBox(false); renderer.setToolTipGenerator(new BoxAndWhiskerToolTipGenerator()); final CategoryPlot plot = new CategoryPlot(dataset, xAxis, yAxis, renderer); final JFreeChart chart = new JFreeChart( "Box-and-Whisker Demo", new Font("SansSerif", Font.BOLD, 14), plot, true ); final ChartPanel chartPanel = new ChartPanel(chart); chartPanel.setPreferredSize(new java.awt.Dimension(450, 270)); setContentPane(chartPanel); } /** * Creates a sample dataset. * * @return A sample dataset. */ private BoxAndWhiskerCategoryDataset createSampleDataset() { final int seriesCount = 2; final int categoryCount = 4; double[] data = null; final DefaultBoxAndWhiskerCategoryDataset dataset = new DefaultBoxAndWhiskerCategoryDataset(); for (int i = 0; i < seriesCount; i++) { if(i == 0) { data = new double[]{2,4,6,8,12,14,16,18,20,25,45}; } else { data = new double[]{2,4,6,8,12,14,16,18,20,25,26}; } for (int j = 0; j < categoryCount; j++) { final List list = new ArrayList(); for (int k = 0; k < data.length; k++) { list.add(new Double(data[k])); } dataset.add(list, "Series " + i, " Type " + j); } } return dataset; } /** * For testing from the command line. * * @param args ignored. */ public static void main(final String[] args) { final BoxAndWhiskerDemo demo = new BoxAndWhiskerDemo("Box-and-Whisker Chart Demo"); demo.pack(); RefineryUtilities.centerFrameOnScreen(demo); demo.setVisible(true); } }