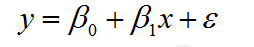R語言學習之簡單線性迴歸
從許多方面來看,迴歸分析都是統計學的核心。它其實是一個廣義的概念,通指那些用一個或多個預測變數(也稱自變數或解釋變數)來預測響應變數(也稱因變數、效標變數或結果變數)的方法。即通過已知的點來建立擬合模型,用給定的X值來預測Y值,找到一條合適的擬合曲線,算出合適的斜率和方差。只有一個自變數的情況稱為簡單迴歸,大於一個自變數情況的叫做多元迴歸。
線性模型:
其中β0和β1是迴歸係數,ε表示誤差。
在R中,擬合線性模型最基本的函式就是lm()。
例項:
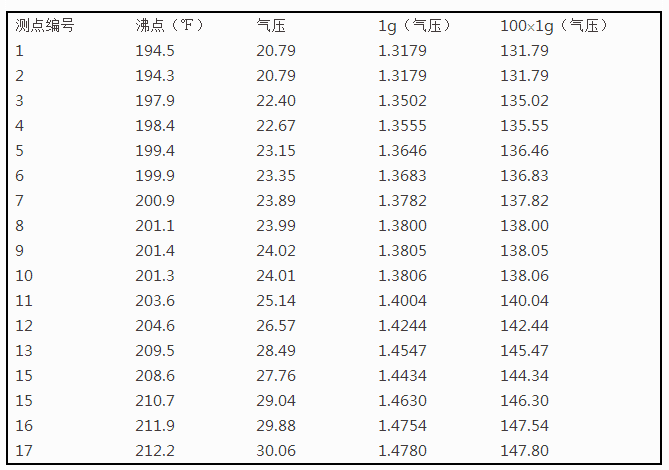
物理學家James.D.Forbes試圖通過水的沸點來估計海拔高度,他知道通過氣壓計測得的大氣壓可用於得到海拔高度,氣壓越低,高度越高,他測量了
首先錄入資料:
x=matrix(c(194.5,20.79,1.3179,131.79,194.3,20.79,1.3179,131.79,197.9,22.40,1.3502,
135.02,198.4,22.67,1.3555,135.55,199.4,23.15,1.3646,136.46,199.9,23.35,
1.3683,136.83,200.9,23.89,1.3782,137.82,201.1,23.99,1.3800,138.00,201.4,
24.02,1.3806,138.06,201.3,24.01,1.3805,138.05,203.6,25.14,1.4004,140.04,
204.6,26.57,1.4244,142.44,209.5,28.49,1.4547,145.47,208.6,27.76,1.4434,
144.34,210.7,29.04,1.4630,146.30,211.9,29.88,1.4754,147.54,212.2,30.06,
1.4780,147.80),ncol=4,byrow=T,dimnames=list(1:17,c('F','h','log','log100')))
資料結果為:
forbes=as.data.frame(x) #強制轉換為資料框
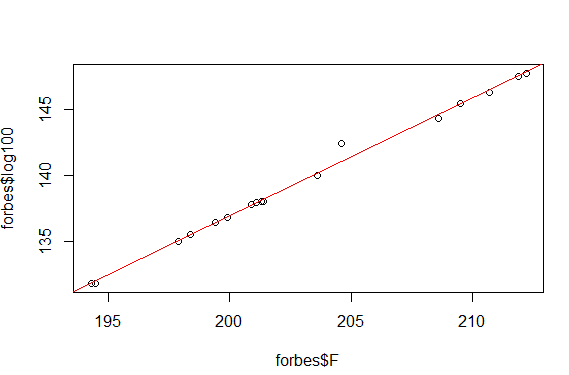
plot(forbes$F,forbes$log100) #檢視F和log100之間的關係
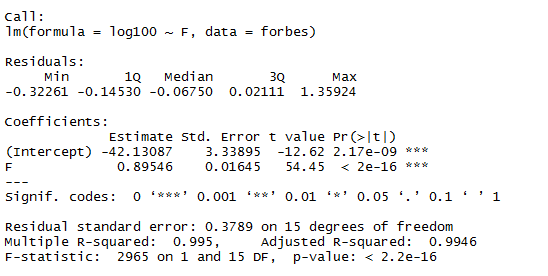
lm.sol=lm(log100~F,data=forbes) #擬合模型
summary(lm.sol)
abline(lm.sol,col="red")
可以得出預測模型為:
y = -42.13087 + 0.89546x
殘差分析:
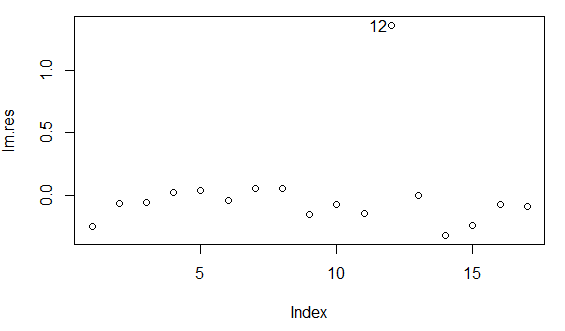
lm.res <- residuals(lm.sol) #殘差分析
plot(lm.res)
text(12,lm.res[12],labels=12,adj=1.2)
identify(lm.res)
由圖中可發現 12 那點偏離比較遠,對結果影響較大,可以把奇異點剔除掉。
lm.up <- lm(log100~F,data=forbes,subset = -12)
summary(lm.up)
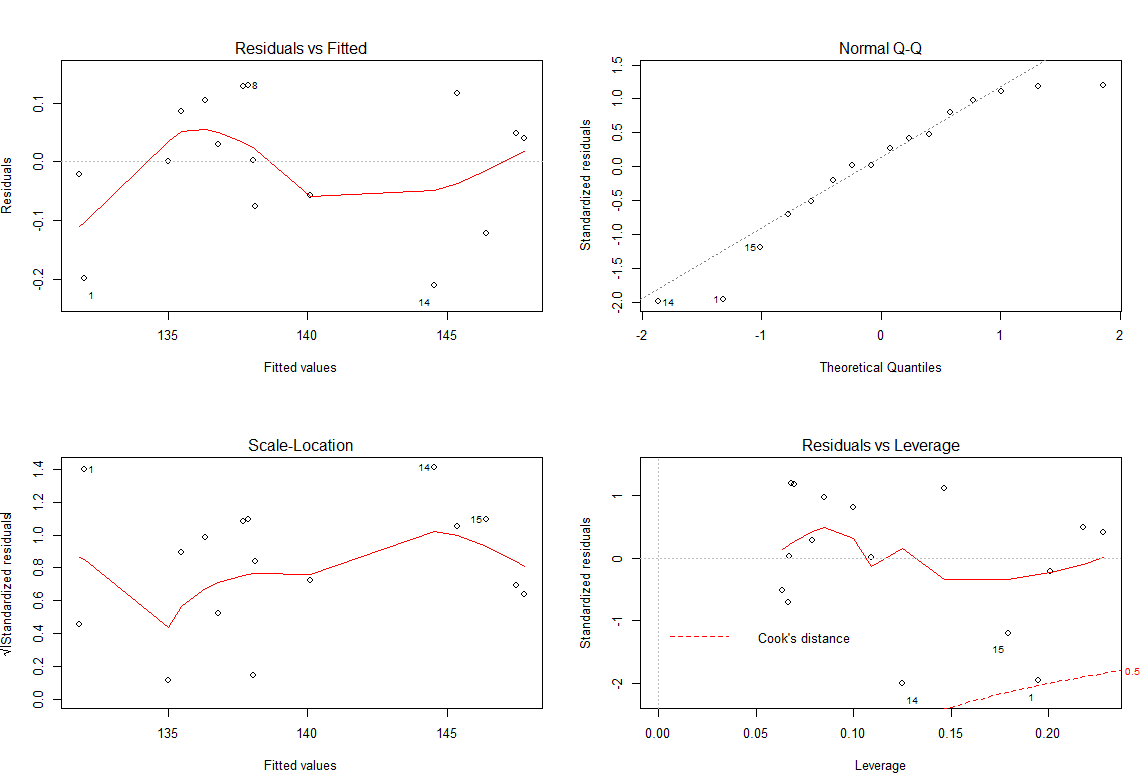
模型診斷:
par(mfrow=c(2,2))
plot(lm.up)