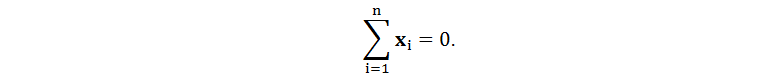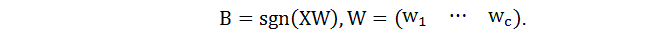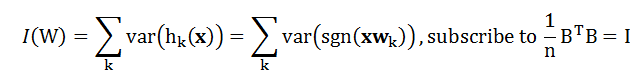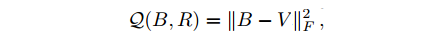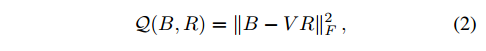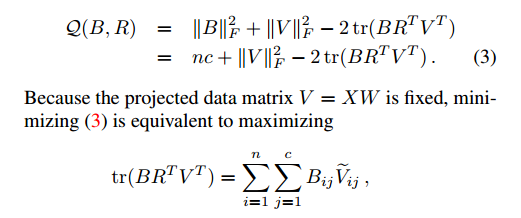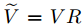影象檢索----迭代量化(Iterative Quantization)理解
一.目標
資料集為: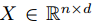
通過c個函式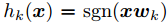
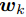
其中sgn函式是對矩陣的元素級操作,得到的是同樣大小的矩陣。ITQ的目標就是學習一個編碼矩陣: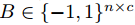
二.演算法推導過程
在應用ITQ演算法之前要對資料做PCA降維,把資料從d維降到c維,編碼時編碼長度就是c維。
什麼樣的二進位制編碼才是好的編碼呢?所有位(總共c位編碼)上編碼的結果要滿足編碼為-1(實際上使用的是0而不是-1)和1的樣本數相等且各位上編碼應該是不相關的(否則出現編碼冗餘了)。而編碼0和1的樣本數相等等價於編碼值的方差最大。即:
但是上式中含有sng(xw)函式不好處理,於是採用一種signed magnitude relaxation技術,將上式化為:
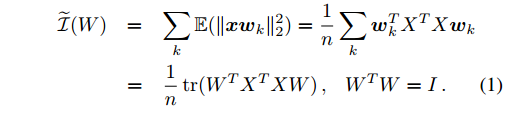
這樣就講一個離散的目標函式轉化為一個連續的目標函式。這個式子跟PCA的目標式很像。
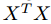 就是樣本的協方差矩陣。因此,要找到協方差矩陣的前c個特徵值對應的特徵向量作為W。
就是樣本的協方差矩陣。因此,要找到協方差矩陣的前c個特徵值對應的特徵向量作為W。
另外,假設實數空間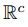
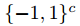
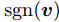
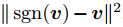
由於跡具有性質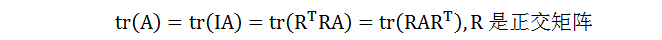
目標式中使用的是F範數,即矩陣各元素的平方和再開根號。
但是Jegou et al發現不使用正交矩陣R,而僅僅使用一個隨機旋轉矩陣R也取得了很好的結果,而找一個隨機旋轉矩陣R要比找正交矩陣簡單得多。
三.推導步驟
1.降維。
在上述推導的指導下,先將資料從d維降到c維,然後使用RR(random rotate)方法找個旋轉矩陣R,大小為c*c(實際中可以先隨機生成一個矩陣,然後做SVD分解,用S作為旋轉矩陣),右乘到降維後的資料V,最小化目標式(2)求得一個粗糙解。下面開始應用ITQ演算法迭代新R,使得目標式(2)的值減少。
2.固定R,更新B。
從上面可以看到最小化(3)式等價於最大化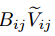
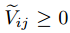 時更新
時更新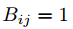 ,否則更新
,否則更新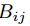 為0。
為0。
3.固定B,更新R。
當B固定時求解這個(2)目標式的最小值就是一個Orthogonal Procrustes problem。於是,先對矩陣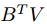
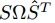
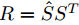
4)分支判斷。
迭代次數是否達到50次,如果沒有,則回到第2步;如果達到了,就結束迴圈。計算最後得到的編碼就是sgn(XWR),大小為n*c。
參考文獻:
1.Gong Y, Lazebnik S. Iterative quantization: A procrustean approach to learning binary codes[C]//Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on. IEEE, 2011: 817-824.