揭開知識庫問答KB-QA的面紗4·向量建模篇
內容速覽
- 向量建模的核心思想
- 如何用分散式表達表示答案和問題
- 如何訓練分散式表達
- 論文實驗與總結
 本期我們將介紹KB-QA傳統方法之一的向量建模(Vector Modeling),我們以一個該方法的經典代表作為例,為大家進一步揭開知識庫問答的面紗。該方法來自Facebook公司Bordes A, Chopra S, Weston J的論文 Question answering with subgraph embeddings(文章發表於2014年的EMNLP會議)。
本期我們將介紹KB-QA傳統方法之一的向量建模(Vector Modeling),我們以一個該方法的經典代表作為例,為大家進一步揭開知識庫問答的面紗。該方法來自Facebook公司Bordes A, Chopra S, Weston J的論文 Question answering with subgraph embeddings(文章發表於2014年的EMNLP會議)。向量建模的核心思想
向量建模方法的思想和資訊抽取的思想比較接近。首先根據問題中的主題詞在知識庫中確定候選答案。把問題和候選答案都對映到一個低維空間
此時,你的心中可能會出現兩個問題,一是如何將問題和答案對映到低維空間,顯然我們不能僅僅將自然語言的問題和答案進行對映,還要將知識庫裡的知識也對映到這個低維空間中(否則我們就只是在做QA而非KB-QA了)。第二個問題是,如果做過類似工作(one-shot,imgae caption,word embedding等)的朋友應該知道,使用這種方法是需要大量資料
接下來,就讓我們帶著這兩個問題,一起看看作者是怎麼解決的。
如何用分散式表達表示答案和問題
問題的分散式表達:首先我們把自然語言問題進行向量化,作者將輸入空間的維度N設定為字典的大小+知識庫實體數目+知識庫實體關係數目,對於輸入向量每一維的值設定為該維所代表的單詞(當然這一維也可能代表的是某個實體數目或實體關係,對於問題的向量化,這些維數都設定為0)在問題中出現的次數(一般為0或1次),可以看出這是一種multi-hot的稀疏表達,是一種簡化版的詞袋模型(Bag-of-words model)。
我們用代表問題,用
代表N維的問題向量,用矩陣
將N維的問題向量對映到
維的低維空間,那麼問題的分散式表達即
答案的分散式表達:我們想想可以怎樣對答案進行向量化,最簡單的方式,就是像對問題一樣的向量化方式,使用一個簡化版的詞袋模型。由於答案都是一個知識庫實體,那麼這樣的表達就是一個one-hot的表達,顯然,這種方式並沒有把知識庫的知識引入到我們的輸入空間中。
第二種方式,我們把知識庫想象成一個圖,圖的節點代表實體,邊代表實體關係。通過問題中的主題詞可以定位到圖中的一個節點,該節點到答案節點有一條路徑,我們把該路徑上的所有邊(實體關係)和點(實體)都以multi-hot的形式存下來作為答案的輸入向量。我們這裡只考慮一跳(hop)或者兩跳的路徑,如路徑(barack obama, place of birth, honolulu)是一跳,路徑(barack obama, people.person.place of birth, location.location.containedby, hawaii) 是兩跳。因此這種表示是一種3-hot或4-hot的表示。
第三種方式,讓我們回想一下我在揭開知識庫問答KB-QA的面紗3·資訊抽取篇介紹的資訊抽取的方法,對於每一個候選答案,該答案所對應的屬性(type/gender等)和關係都是能夠幫助我們判斷它是否是正確答案的重要資訊,因此我們可以把每個候選答案對應的知識庫子圖(1跳或2跳範圍)也加入到輸入向量中,假設該子圖包含C個實體和D個關係,那麼我們最終的表達是一種3+C+D-hot或者4+C+D-hot的表達。和資訊抽取方法一樣,我們也對關係的方向進行區分,因此我們輸入向量的大小變為字典的大小+2*(知識庫實體數目+知識庫實體關係數目)。
同樣的,我們用表示答案,用
表示答案的輸入向量,用矩陣
將問題向量對映到
維的低維空間,答案的分散式表達即
。
向量得分:最後我們用一個函式表徵答案和問題的得分,我們希望問題和它對應的正確答案得儘量高分,通過比較每個候選答案的得分,選出最高的,作為正確答案。得分函式定義為二者分散式表達的點乘,即。
上述整個流程如下圖所示

如何訓練分散式表達
對於訓練資料集,我們一個定義margin-based ranking損失函式,公式如下
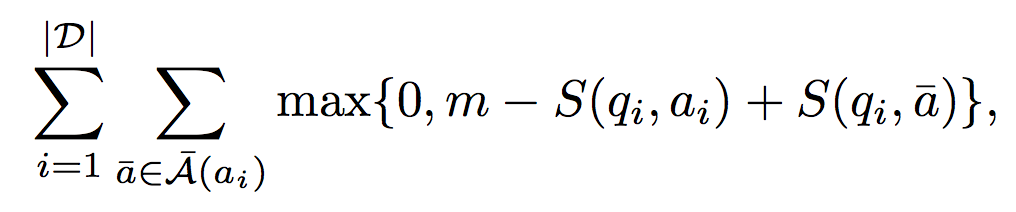 做過zero-shot或者對SVM瞭解的朋友應該對這個式子不會陌生,其中
做過zero-shot或者對SVM瞭解的朋友應該對這個式子不會陌生,其中和訓練word embedding一樣,為減少計算量,我們通過取樣的方式構造負樣本,50%來自隨機挑選,50%來自與問題主題詞實體相連的其它路徑。
由於benchmark資料集WebQuestion包含的樣本數過少,作者還構造了其他幾個資料集:
Freebase:選取freebase中包含出現頻率高於5次實體的三元組,得到一個知識庫子集(含2.2M實體和7K關係),對於每一個三元組如(subject, type1.type2.predicate, object),我們通過自動化的方式,生成這樣的問題答案對:
Quesiton:“What is the predicate of the type2subject?” Answer:object
ClueWeb Extractions: 由於 Freebase的三元組都是形式化語言,並不貼近自然語言,我們也用同樣的方式將ClueWeb上提取出的三元組(subject, “text string”, object)通過少量模板作同樣的變換(作者提取了2M對三元組)。
這樣我們就在WebQuestion資料集的基礎上,得到了一個新的擴充套件資料集,該資料集的例子如下表所示:
 可以看出,擴增版的資料集,問題大多數都是自動構造的,缺乏多樣性和真實性。怎麼辦呢?我們希望訓練資料中問題的分散式表達儘量貼近它所類似的真實問題的分散式表達。因此,作者在WikiAnswers中抓取了2.2M問題(不含答案),通過問題的分類標籤,將它們分為了350k個類簇(可以理解為每個類簇裡的自然語言問題它所表達的意思是一樣的)。如下表所示
可以看出,擴增版的資料集,問題大多數都是自動構造的,缺乏多樣性和真實性。怎麼辦呢?我們希望訓練資料中問題的分散式表達儘量貼近它所類似的真實問題的分散式表達。因此,作者在WikiAnswers中抓取了2.2M問題(不含答案),通過問題的分類標籤,將它們分為了350k個類簇(可以理解為每個類簇裡的自然語言問題它所表達的意思是一樣的)。如下表所示
接下來我們就可以進行一個多工學習(multi-task),讓同一個類簇的問題得分較高,即,其訓練方式和之前訓練答案和問題得分是一樣的。
至此,通過以上兩種訓練,我們的分散式表達就訓練完畢了。
論文實驗與總結
根據問題首先要確定候選答案,這裡作者確定候選答案的方式和資訊抽取略有不同。首先在從問題中主題詞對應的知識庫實體出發,通過beam search的方式儲存10個和問題最相關的實體關係(通過把實體關係當成答案,用式子的得分作為beam search的排序標準)。接下來選取主題詞兩跳範圍以內的路徑,且該路徑必須包含這10個關係中的關係,將滿足條件的路徑的終點對應的實體作為候選答案,其中,1跳路徑的權值是2跳的1.5倍(因為2跳包含的元素更多)。
確定完候選答案後,選取得分最高的作為最終答案。
該方法在WebQuestion資料集上進行測試,取得了39.2的F1-Score。
可以看出,相比資訊抽取和語義解析的方法,該方法幾乎不需要任何手工定義的特徵(hand- crafted features),也不需要藉助額外的系統(詞彙對映表,詞性標註,依存樹等)。相對來說,比較簡單,也較容易實現,能取得39.2的F1-score得分(斯坦福13年的語義解析方法只有35.7)也說明了該方法的強大性。通過自動化的方式擴充套件資料集和多工訓練也部分解決了實驗資料不足的缺點。
然而,向量建模方法,是一種趨於黑盒的方法,缺少了解釋性(語義解析可以將問題轉化成一種邏輯形式的表達,而資訊抽取構造的每一維特徵的含義也是離散可見的),更重要的是,它也缺少了我們的先驗知識和推理(可以看出其F1-score略低於14年使用了大量先驗知識的資訊抽取方法,該方法F1-score為42.0),事實上,這也是現在深度學習一個比較有爭議的詬病。
就篇論文的向量建模方法來說,也存在一些問題,比如對問題的向量表示採用了類似詞袋模型的方法,這樣相當於並未考慮問題的語言順序(比如 “謝霆鋒的爸爸是誰?” 謝霆鋒是誰的爸爸? 這兩個問題用該方法得到的表達是一樣的,然而這兩個問題的意思顯然是不同的),且訓練分散式表達的模型很簡單,相當於一個兩層的感知機。這些問題,可以通過深度學習來解決。
隨著深度學習的加入,KB-QA進入了一個新的時代。下一期,我們將進入深度學習篇,由於深度學習可以對傳統的三種方法都可以進行提升,因此我打算將深度學習篇拆成2~3篇來進行講解,進一步揭開KB-QA的面紗。
敬請期待。
https://zhuanlan.zhihu.com/p/25824501
