一直沒搞懂非平衡二叉樹變平衡二叉樹時左旋右旋，今天下定決心搞懂，然後在眾多部落格中終於找到了這樣一篇，非常形象，記錄如下：

AVL樹是最先發明的自平衡二叉查詢樹。在AVL樹中任何節點的兩個子樹的高度最大差別為一，所以它也被稱為高度平衡樹。查詢、插入和刪除在平均和最壞情況下都是O（log n）。增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。AVL樹得名於它的發明者G.M. Adelson-Velsky和E.M. Landis，他們在1962年的論文《An algorithm for the organization of information》中發表了它。

節點的平衡因子是它的左子樹的高度減去它的右子樹的高度（有時相反）。帶有平衡因子1、0或 -1的節點被認為是平衡的。帶有平衡因子 -2或2的節點被認為是不平衡的，並需要重新平衡這個樹。平衡因子可以直接儲存在每個節點中，或從可能儲存在節點中的子樹高度計算出來。

AVL樹的基本操作一般涉及運作同在不平衡的二叉查詢樹所運作的同樣的演算法。但是要進行預先或隨後做一次或多次所謂的"AVL旋轉"。

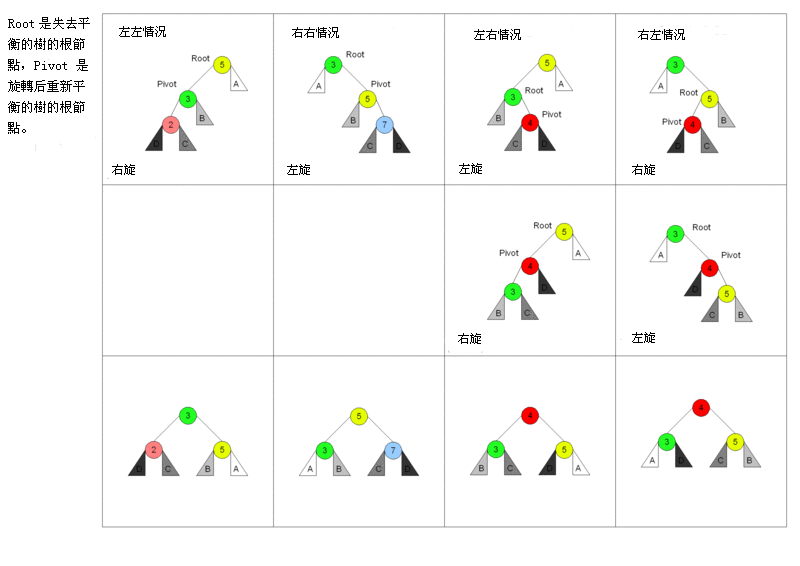
    從圖中可以比較形象的看出所謂左旋右旋的旋轉支點是三個主節點中大小居中的那個節點，左旋就是左邊的節點降下來，右旋就是右邊的節點降下來，都成為中間節點的子樹。

左右雙旋分解就是先將左側節點降為左子樹，右邊節點將為右子樹。當然中間有合併子樹的過程，這裡沒有細說。

高度為h的AVL樹，節點數N最多； 最少 ( 其中 )N是h的斐波那契數列。