題目發出後，大家的迴應似乎比我想象中的更積極，我看到了好幾個不同的正確解答。加上我本來知道的幾種做法，現在我已經知道了至少5種正確的解法。現在隨便發一個，供大家參考。

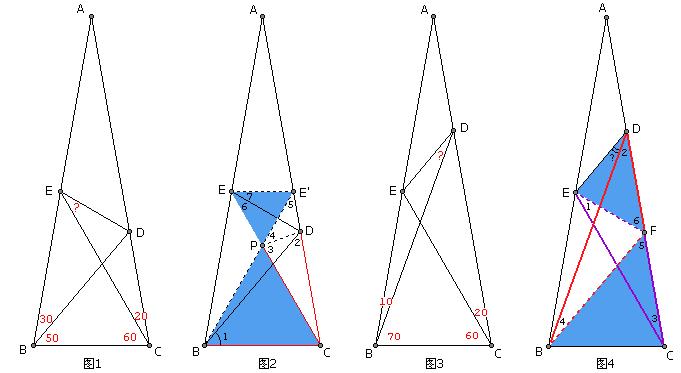
    我們首先從號稱世界第二難的幾何題“50-60三角形”（圖一）入手。這個題目要稍微簡單一些，因為有個已知條件很重要：∠1=50°=∠2，因此我們一開始就有了一個等腰三角形，其中BC=CD。過E作BC的平行線交AC於E'（圖二），我們很快就可以知道兩個藍色三角形是等邊三角形，於是BC=CP。這樣的話三條紅色線段都相等，△CPD是等腰三角形，即可算出∠3=80°，∠4=40°。而△BE'C中的∠5也是40°，於是△DPE'也是等腰三角形，DP=DE'。又EP=EE'（全等三角形的兩邊），ED=ED（公共邊），因此△DEE'=△DEP。∠6=∠7=1/2∠PEE'=30°

    事實上，利用50-60問題的結論，我們能很快解決60-70問題（圖三）。在AC上找一點F使得∠CBF=50°（圖4），根據前面的結論，∠1=30°。而△BDC中的∠2也是30°。又∠3=∠4=20°，於是紅色三角形和紫色三角形相似，CF/EF=BF/DF。而∠5=50°，∠6=∠1+∠3=50°，結合前面的比例關係，於是兩個藍色三角形相似。這樣的話，∠EDF=∠CBF=50°。我們要求的角就等於∠EDF-∠2=20°

    解答很繁瑣。目前我還沒有找到什麼簡單而巧妙的解法。歡迎大家提供更多的解答思路。