圓點博士小四軸演算法快速入門--四元數和PID圖解
阿新 • • 發佈:2019-01-03
參考http://www.eeboard.com/bbs/thread-32321-1-1.html
飛控的演算法程式碼一般包括下面三個部分:濾波,姿態,PID
1,濾波可以用互補濾波來實現,互補濾波的資料很多,大家隨便就能找到。基本公式是: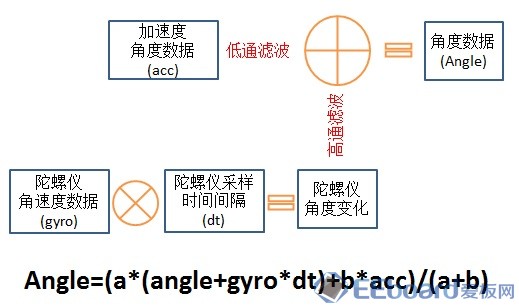
2,濾波完就是四元數拉。直接用老外Madgwick的IMU就可以。超級簡單
unsigned char BS004_IMU_Update(float ax,float ay,float az,float gx,float gy,float gz)
{
float norm;
float vx, vy, vz;
float ex, ey, ez;
//
//圓點博士:四元數乘法運算
float q0q0 = q0 * q0;
float q0q1 = q0 * q1;
float q0q2 = q0 * q2;
float q1q1 = q1 * q1;
float q1q3 = q1 * q3;
float q2q2 = q2 * q2;
float q2q3 = q2 * q3;
float q3q3 = q3 * q3;
//
//圓點博士:歸一化處理
norm = sqrt(ax*ax + ay*ay + az*az);
if(norm==0) return 0;
ax = ax / norm;
ay = ay / norm;
az = az / norm;
//
//圓點博士:建立小四軸座標系
vx = 2*(q1q3 - q0q2);
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3;
//
//圓點博士:座標系和重力叉積運算
ex = (ay*vz - az*vy);
ey = (az*vx - ax*vz);
ez = (ax*vy - ay*vx);
//
//圓點博士:比例運算
exInt = exInt + ex*bs004_quad_Ki;
eyInt = eyInt + ey*bs004_quad_Ki;
ezInt = ezInt + ez*bs004_quad_Ki;
//
//圓點博士:陀螺儀融合
gx = gx + bs004_quad_Kp*ex + exInt;
gy = gy + bs004_quad_Kp*ey + eyInt;
gz = gz + bs004_quad_Kp*ez + ezInt;
//
//圓點博士:整合四元數率
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*bs004_quad_halfT;
q1 = q1 + (q0*gx + q2*gz - q3*gy)*bs004_quad_halfT;
q2 = q2 + (q0*gy - q1*gz + q3*gx)*bs004_quad_halfT;
q3 = q3 + (q0*gz + q1*gy - q2*gx)*bs004_quad_halfT;
//
//圓點博士:歸一化處理
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
if(norm==0) return 0;
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
//
//圓點博士:尤拉角轉換
bs004_imu_roll=asin(-2*q1q3 + 2*q0q2)*57.30f;
bs004_imu_pitch=atan2(2*q2q3 + 2*q0q1, -2*q1q1-2*q2q2 + 1)*57.30f;
bs004_imu_yaw=bs004_imu_yaw-gz*bs004_mpu6050_gyro_scale;
//
return 1;
}
3, PID的程式碼其實也很簡單,主要是要了解其中的原理,才能更好地調整引數。為了方便新手們理解,樓主建立了一個數學模型來讓大家瞭解。(只針對新手,老手就算了)
========圓點博士小四軸之PID控制模式分析=======
PID控制的P是Proportional的縮寫, 是比例的意思,I是Integral的縮寫,是積分的意思,D是Derivative的縮寫,是微分的意思。所以,PID就是我們常說的比例,積分,微分控制。
我們首先來看一個PID控制模型曲線圖:
該圖包含了比例控制,比例+積分控制,比較+積分+微分控制的電機響應圖的對比。
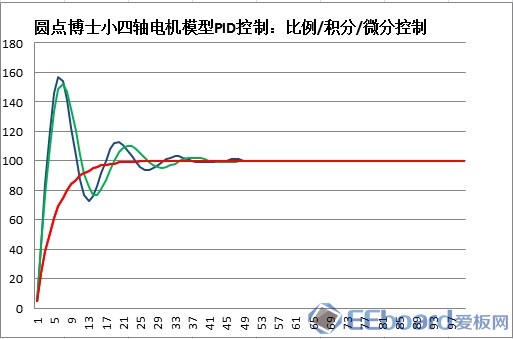
下面我們對曲線進行具體分析:
PID中的比例控制是最容易理解的,比例控制就是把角度的誤差乘以一個常數作為輸出驅動。假定我們有一個理想模型的電機,1V電壓的變化會帶來小四軸1度的角度改變。假定現在電機控制電壓是5V,小四軸在某一軸上的偏角是5度,目標角度是100度。我們把當前的電壓量定義為Vin,把輸出控制量定義為Vout。假定P等於0.2,那麼比例控制的結果就是:
第一次:Vout=Vin+(100-5)*P=5V+19V=24V,得到電機電壓是24V,對應的小四軸角度是24度,距離目標角度的誤差是100-24=76度。
第二次:Vout=Vin+(100-24)*P=24V+15V=39V, 從而引起的角度是39度。
我們看到,在這麼的一個比例控制系統下,小四軸角度在慢慢地向目標角度靠近。
PID中的積分控制就是把把所有角度誤差相加起來,然後乘上一個常數作為輸出驅動。在上述例子中,假定I=0.2, 我們來看看比例和積分控制同時起作用下的系統反應。
第一次:Vout=Vin+(100-5)*P+(100-5)*I=5V+19V+19V=43V,這時候小四軸角度為43度。
由於第一次控制前的誤差是100-5=95,第二次控制前的誤差是100-43=57,所以積分結果是152。
第二次:Vout=Vin+(100-43)*P+((100-5)+(100-43))*I=43V+11V+30V=84V, 這時候小四軸角度變為84度。
第三次:Vout=Vin+(100-84)*P+((100-5)+(100-43)+(100-84))*I=84+3V+33V=120V。這時小四軸角度變為120度。
我們看到,在增加了積分控制後,小四軸角度在快速向目標角度靠近。
PID中的微分控制就是把角度的變化乘上一個常數來作為電機驅動輸出。在上述例子中,假定D=0.2, 我們來看看比例,積分和微分共同控制下的系統反應。假定第一次前,電機轉速保持5轉,那麼第一次前的角度變化為0。
第一次:Vout=Vin+(100-5)*P+(100-5)*I-(5-5)*D=5V+19V+19V-0V=43V,這時候小四軸角度為43度。
和上一次相比,角度從5度變化到了43度,所以小四周角度變化是43-5=38度。
第二次:Vout=Vin+(100-43)*P+((100-5)+(100-43))*I-(43-5)*D=43V+11V+30V-7V=77V, 這時候小四周角度77度。
把上述的計算結果列出來,我們看到:
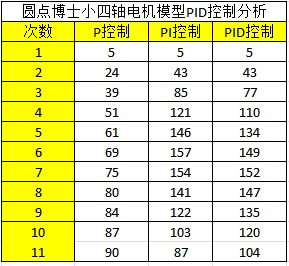
從上面的資料,我們可以看到:
1,單獨比例控制的時候,資料慢慢接近目標 (圖表中的紅色線)
2,加入積分控制之後,資料快速接近目標 (圖表中的藍色線)
3,微分控制起到抑制變化的作用。(圖表中的綠色線)
有了這些理論基礎,就可以寫PID控制程式碼拉。
========圓點博士小四軸之PID控制程式碼分析=======
在圓點博士小四軸2014版程式碼裡,我們只使用到PD引數。
首先我們來看PID中的比例控制。跟上一節模型提到的一樣,比例是針對誤差的控制。
首先我們獲取小四軸當前角度。
bs004_angle_cur_pitch=bs004_imu_pitch;
bs004_angle_cur_roll =bs004_imu_roll;
把當前角度和目標角度相減,就可以得到角度偏差。
bs004_angle_err_pitch=bs004_angle_cur_pitch-bs004_angle_target_pitch;
bs004_angle_err_roll=bs004_angle_cur_roll-bs004_angle_target_roll;
然後進行比例控制:
bs004_fly_m1=bs004_fly_m1
+bs004_pitch_p*bs004_angle_err_pitch
-bs004_roll_p *bs004_angle_err_roll
-bs004_yaw_p*bs004_angle_err_yaw;
bs004_fly_m2=bs004_fly_m2
-bs004_pitch_p*bs004_angle_err_pitch
-bs004_roll_p *bs004_angle_err_roll
+bs004_yaw_p*bs004_angle_err_yaw;
bs004_fly_m3=bs004_fly_m3
-bs004_pitch_p*bs004_angle_err_pitch
+bs004_roll_p *bs004_angle_err_roll
-bs004_yaw_p*bs004_angle_err_yaw;
bs004_fly_m4=bs004_fly_m4
+bs004_pitch_p*bs004_angle_err_pitch
+bs004_roll_p *bs004_angle_err_roll
+bs004_yaw_p*bs004_angle_err_yaw;
在上一節模型中,我們提到PID中的微分控制針對的是角度變化而進行的控制。
所以我們首先要得到當前角度和上一次角度的差異。
bs004_angle_dif_pitch=bs004_angle_cur_pitch-bs004_angle_last_pitch;
bs004_angle_dif_roll =bs004_angle_cur_roll-bs004_angle_last_roll;
bs004_angle_dif_yaw =bs004_angle_last_yaw-bs004_angle_cur_yaw;
然後進行微分控制:
bs004_fly_m1=bs004_fly_m1
+bs004_pitch_d*bs004_angle_dif_pitch
-bs004_roll_d *bs004_angle_dif_roll
-bs004_yaw_d*bs004_angle_dif_yaw;
bs004_fly_m2=bs004_fly_m2
-bs004_pitch_d*bs004_angle_dif_pitch
-bs004_roll_d *bs004_angle_dif_roll
+bs004_yaw_d*bs004_angle_dif_yaw;
bs004_fly_m3=bs004_fly_m3
-bs004_pitch_d*bs004_angle_dif_pitch
+bs004_roll_d *bs004_angle_dif_roll
-bs004_yaw_d*bs004_angle_dif_yaw;
bs004_fly_m4=bs004_fly_m4
+bs004_pitch_d*bs004_angle_dif_pitch
+bs004_roll_d *bs004_angle_dif_roll
+bs004_yaw_d*bs004_angle_dif_yaw;
從上面的描述我們可以看出,小四軸的PID控制還是比較簡單的。
