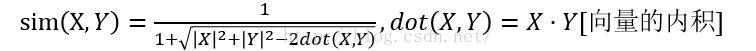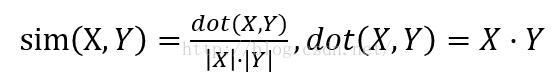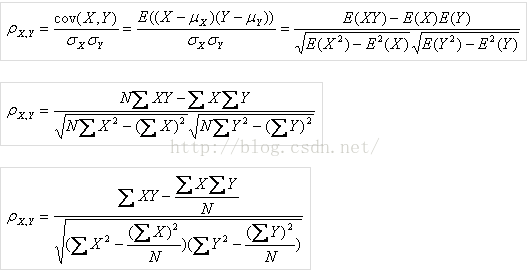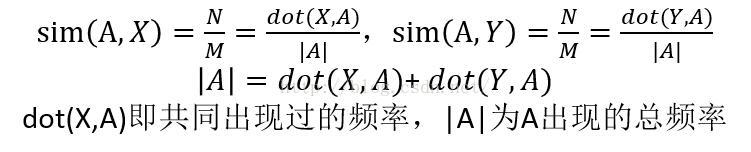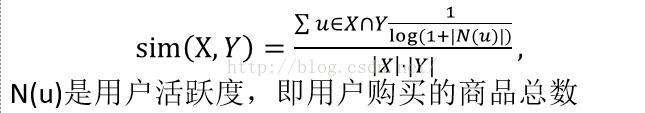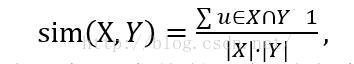推薦系統中相似度演算法介紹及效果測試
阿新 • • 發佈:2019-01-03
######################
尊重版權,轉載註明地址######################
相似度演算法介紹
相似度演算法主要任務是衡量物件之間的相似程度,是資訊檢索、推薦系統、資料探勘等的一個基礎性計算。下面重點介紹幾種比較常用的相似度演算法。
向量表示通常假設物件X和Y都具有N維的特徵,即
X=(x_1,x_2,…x_n) Y=(y_1,y_2,…y_n)
在推薦場景下,假設使用者物品矩陣為:
item1=(0,1,1) item2=(1,0,1)
1.歐氏距離
歐式距離相似度演算法需要保證各個維度指標在相同的刻度級別,比如對身高、體重兩個單位不同的指標使用歐氏距離可能使結果失效。
並且,歐氏距離適合比較稠密的矩陣。
增量計算說明:
•【在計算增量時候,|x|+|y|必然會增大】 •當|x*y|都出現時候,|x|+|y|至少增加了2,兩項抵消,最多是相等,否則分母變大,值會變小 •當|x*y|只出現其中一個,|x+y|至少增加 1,依然是分母變大,值變小。 •規律,隨著增量的增加,該公式一定會讓出現的相似度減小。相反,沒有再出現的物品,x,y,反倒相似度維持不變2.餘弦相似
資料稀疏性強,就考慮用夾角餘弦相似度演算法
缺點:餘弦相似度受到向量的平移影響,上式如果將x平移到x+1,餘弦值就會改變【即當各個物件的評分指標不一致的時候,餘弦相似度不能穩定刻畫其相似,這種情況下使用皮爾遜相似度會更好】
3. 皮爾遜相似度
計算相對比較複雜,只能應用於帶評分的場景,對不同刻度的評分(如一個物件評分集中在4分,另一個集中在3分)衡量相似度時具有良好的效果。在計算相似度時採用了這種方法,近似的可以把最後一個帶N的去掉(預設N很大,作為分母幾乎趨近於0)。出現一次的計為1,出現多次的統一計為2.
4. 簡單粗暴的N/M
應用於元素值為1或者0的向量。
當計算與A相似物件的相似值的時候, 如A與X,Y之間的相似,則計算公式為
計算結果不是特別準,適用於資料量非常龐大,對若干物件的近似估計
5. IUF相似度(基於使用者活躍度倒數的引數)
對比前面的餘弦相似,餘弦相似也可以表示為
這裡即為對每一個值的累加時考慮了使用者的因素。
效果:能推出更多的商品來,提高召回率
相似度演算法效果測試
樣本資料
測試結果

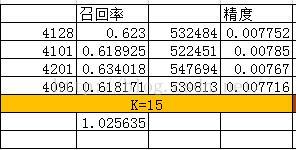
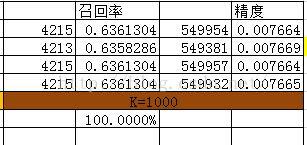
其中: 精度 = 推薦被購買的商品總數 / 總推薦商品數 召回率 = 推薦被購買的商品總數 / 測試集商品數