轉自：http://www.pami.sjtu.edu.cn/people/xzj/introducelle.htm

          http://www.cs.nyu.edu/~roweis/lle/algorithm.html

          http://axon.cs.byu.edu/Dan/678/miscellaneous/Manifold.example.pdf

1 LLE介紹

 Locally linear embedding (LLE) (Sam T.Roweis and Lawrence K.Saul, 2000)以及Supervised locally linear embedding (SLLE) (Dick and Robert, 2002) 是最近提出的非線性降維方法，它能夠使降維後的資料保持原有拓撲結構。

    LLE演算法可以有圖1所示的一個例子來描述。在圖1所示中，LLE能成功地將三維非線性資料對映到二維空間中。如果把圖1（B）中紅顏色和藍顏色的資料分別看成是分佈在三維空間中的兩類資料，通過LLE演算法降維後，則資料在二維空間中仍能保持相對獨立的兩類。在圖1（B）中的黑色小圈中可以看出，如果將黑色小圈中的資料對映到二維空間中，如圖1（C）中的黑色小圈所示，對映後的資料任能保持原有的資料流形，這說明LLE演算法確實能保持流形的領域不變性。由此LLE演算法可以應用於樣本的聚類。而線性方法，如PCA和MDS，都不能與它比擬的。LLE演算法操作簡單，且演算法中的優化不涉及到區域性最小化。該演算法能解決非線性對映，但是，當處理資料的維數過大，數量過多，涉及到的稀疏矩陣過大，不易於處理。在圖1中的球形面中，當缺少北極面時，應用LLE演算法則能很好的將其對映到二維空間中，如圖1中的C所示。如果資料分佈在整個封閉的球面上，LLE則不能將它對映到二維空間，且不能保持原有的資料流形。那麼我們在處理資料中，首先假設資料不是分佈在閉合的球面或者橢球面上。

圖1 非線性降維例項：B是從A中提取的樣本點（三維），通過非線性降維
演算法（LLE），將資料對映到二維空間中（C）。從C圖中的顏色可以看出
通過LLE演算法處理後的資料，能很好的保持原有資料的鄰域特性

    LLE演算法是最近提出的針對非線性資料的一種新的降維方法，處理後的低維資料均能夠保持原有的拓撲關係。它已經廣泛應用於影象資料的分類與聚類、文字識別、多維資料的視覺化、以及生物資訊學等領域中。

2 LLE演算法

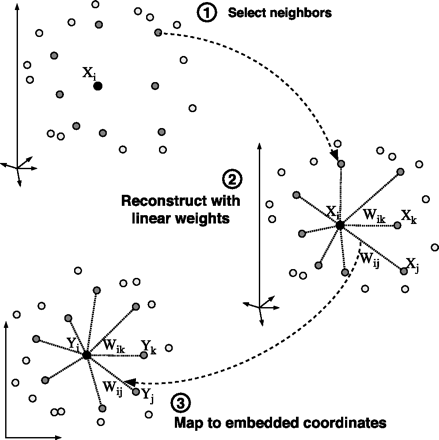
    LLE演算法可以歸結為三步: (1)尋找每個樣本點的k個近鄰點；（2）由每個樣本點的近鄰點計算出該樣本點的區域性重建權值矩陣；（3）由該樣本點的區域性重建權值矩陣和其近鄰點計算出該樣本點的輸出值。具體的演算法流程如圖2所示。

圖2 LLE演算法流程

    演算法的第一步是計算出每個樣本點的k個近鄰點。把相對於所求樣本點距離最近的k個樣本點規定為所求樣本點的 個近鄰點。k是一個預先給定值。Sam T.Roweis 和 Lawrence K.Saul演算法採用的是歐氏距離，則減輕複雜的計算。然而本文是假定高維空間中的資料是非線性分佈的，採用了diijstra距離。Dijkstra 距離是一種測地距離，它能夠保持樣本點之間的曲面特性，在ISOMAP演算法中有廣泛的應用。針對樣本點多的情況，普通的dijkstra演算法不能滿足LLE演算法的要求。

    LLE演算法的第二步是計算出樣本點的區域性重建權值矩陣。這裡定義一個誤差函式，如下所示：

其中 為 的k個近鄰點， 是 與 之間的權值，且要滿足條件： 。這裡求取W矩陣，需要構造一個區域性協方差矩陣  。

    將上式與相結合，並採用拉格朗日乘子法，即可求出區域性最優化重建權值矩陣：

    在實際運算中，可能是一個奇異矩陣，此時必須正則化，如下所示：

其中r是正則化引數，I是一個kxk的單位矩陣。

    LLE演算法的最後一步是將所有的樣本點對映到低維空間中。對映條件滿足如下所示：

其中，為損失函式值，是的輸出向量，是的k個近鄰點，且要滿足兩個條件，即：

其中I是的單位矩陣。這裡的可以儲存在的稀疏矩陣W中，當是的近鄰點時，，否則，。則損失函式可重寫為：

其中M是一個的對稱矩陣,其表示式為:

要使損失函式值達到最小, 則取Y為M的最小m個非零特徵值所對應的特徵向量。在處理過程中，將M的特徵值從小到大排列，第一個特徵值幾乎接近於零，那麼捨去第一個特徵值。通常取第間的特徵值所對應的特徵向量作為輸出結果。

3.LLE Algorithm Pseudocode

nput X: D by N matrix consisting of N data items in D dimensions.
Output Y: d by N matrix consisting of d < D dimensional embedding coordinates for the input points.

1. Find neighbours in X space [b,c].

   for i=1:N
     compute the distance from Xi to every other point Xj
     find the K smallest distances 
     assign the corresponding points to be neighbours of Xi
   end
   

2. Solve for reconstruction weights W.

   for i=1:N
     create matrix Z consisting of all neighbours of Xi [d]
     subtract Xi from every column of Z
     compute the local covariance C=Z'*Z [e]
     solve linear system C*w = 1 for w [f]
     set Wij=0 if j is not a neighbor of i
     set the remaining elements in the ith row of W equal to w/sum(w);
   end
   

3. Compute embedding coordinates Y using weights W.

   create sparse matrix M = (I-W)'*(I-W)
   find bottom d+1 eigenvectors of M
     (corresponding to the d+1 smallest eigenvalues) 
   set the qth ROW of Y to be the q+1 smallest eigenvector
     (discard the bottom eigenvector [1,1,1,1...] with eigenvalue zero)

4.一個例子