今天在學習貝塞爾曲線看到需要結合三角函式 以及兩個不認識的Api
:API Math.atan() 和Math.atan2()

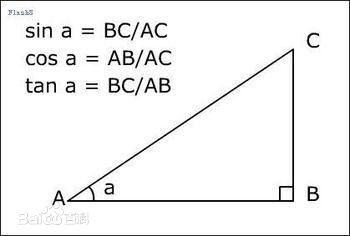
先看下三角函式

正切函式圖:(180為一個週期 即45=45+180)

正弦
正餘弦函式方程為：
y = Asin(wx+b)+h ，這個公式裡：w影響週期，A影響振幅，h影響y位置，b為初相；

w:週期就是一個完整正弦曲線圖此數值越大sin的週期越小 (cos越大)
A:振幅兩個山峰最大的高度.如果A越大兩個山峰越高和越低

h:你正弦曲線和y軸相交點.(影響正弦圖初始高度的位置)

b:初相會讓你圖片向x軸平移

餘弦

Math.atan() 和Math.atan2()
我們可以使用正切操作將角度轉變為斜率,那麼怎樣利用斜率來轉換為角度呢?可以利用斜率的反正切函式將他轉換為相應的角度.as中有兩個函式可以計算反正切,我們來看一下.
1、as中Math.atan()
Math.atan()接受一個引數:用法如下:
angel=Math.atan(slope)
angel為一個角度的弧度值,slope為直線的斜率,是一個數字,這個數字可以是負的無窮大到正無窮大之間的任何一個值.
不過,利用他進行計算比較複雜.因為他的週期性,一個數字的反正切值不止一個.例如atan(-1)的值可能是45度,也可能是225度.這樣就是他的週期性,對於正切函式來說,他的週期是180度,所以兩個相差180度的角具有相同的正切和斜率:
tanθ=tan(θ+180)
然而,Math.atan()只能返回一個角度值,因此確定他的角度非常的複雜,而且,90度和270度的正切是無窮大,因為除數為零,我們也是比較難以處理的~!因此我們更多的會採用第二個函式.
2、Math.atan2()
Math.atan2()接受兩個引數x和y,方法如下:
angel=Math.atan2(y,x)
x 指定點的 x 座標的數字。
y 指定點的 y 座標的數字。
計算出來的結果angel是一個弧度值,也可以表示相對直角三角形對角的角，其中 x 是臨邊邊長，而 y 是對邊邊長。
下面我們來測試一下這兩個函式:
x=Math.atan(1)//計算正切值為1的數字對應的弧度值
trace(x) //輸出一個弧度值0.785398163397448
x=180*x/Math.PI//轉換為角度值
trace(x) //輸出45
x=Math.atan2(7,7)
trace(x)//輸出0.785398163397448
x=180*x/Math.PI//轉換為角度值
trace(x)//輸出45
x=Math.atan2(7,-7)
trace(x)2.35619449019234
x=180*x/Math.PI//轉換為角度值
trace(x)135
x=Math.atan2(-7,7)
trace(x)//輸出-0.785398163397448
x=180*x/Math.PI//轉換為角度值
trace(x)//輸出-45
x=Math.atan2(-7,-7)
trace(x)//輸出-2.35619449019234
x=180*x/Math.PI//轉換為角度值
trace(x)//輸出-135
//從這些測試可以看出,通過座標系的自動調整,我們可以很自由的計算出處於不同象限的位置相對應的角度.
3、計算兩點間連線的傾斜角.
這種方法非常的有用.
Math.atan2()函式返回點(x,y)和原點(0,0)之間直線的傾斜角.那麼如何計算任意兩點間直線的傾斜角呢?只需要將兩點x,y座標分別相減得到一個新的點(x2-x1,y2-y1).然後利用他求出角度就可以了.使用下面的一個轉換可以實現計算出兩點間連線的夾角.
Math.atan2(y2-y1,x2-x1)
不過這樣我們得到的是一個弧度值,在一般情況下我們需要把它轉換為一個角度.
下面我們用一段程式碼來測試一下這樣的轉換.
//測試,計算點(3,3)和(5,5)構成的連線的夾角
x=Math.atan2(5-3,5-3)
trace(x)//輸出0.785398163397448
x=x*180/Math.PI//轉換為角度
trace(x)//輸出45

弧度轉角度
// 用角度表示的角
B = Math.toDegrees(B);
角度轉弧度
public static double toRadians(double angdeg)