希爾排序

Shellsort with gaps 23, 10, 4, 1 in action.
分類	排序演算法
資料結構	陣列
最差時間複雜度	根據步長序列的不同而不同。 已知最好的: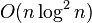
最優時間複雜度	O(n)
平均時間複雜度	根據步長序列的不同而不同。
最差空間複雜度	O(n)
最佳演算法	非最佳演算法
查 ·論 ·編

希爾排序，也稱遞減增量排序演算法，是插入排序的一種高速而穩定的改進版本。

希爾排序是基於插入排序的以下兩點性質而提出改進方法的：

• 插入排序在對幾乎已經排好序的資料操作時， 效率高， 即可以達到線性排序的效率
• 但插入排序一般來說是低效的， 因為插入排序每次只能將資料移動一位

[編輯]歷史

希爾排序按其設計者希爾（Donald Shell）的名字命名，該演算法由1959年公佈。一些老版本教科書和參考手冊把該演算法命名為Shell-Metzner，即包含Marlene Metzner Norton的名字，但是根據Metzner本人的說法，“我沒有為這種演算法做任何事，我的名字不應該出現在演算法的名字中。”

[編輯]演算法實現

原始的演算法實現在最壞的情況下需要進行O(n²)的比較和交換。V. Pratt的書^[1]對演算法進行了少量修改，可以使得效能提升至O(nlog²n)。這比最好的比較演算法的O(nlogn)要差一些。

希爾排序通過將比較的全部元素分為幾個區域來提升

假設有一個很小的資料在一個已按升序排好序的陣列的末端。如果用複雜度為O(n²)的排序（氣泡排序或插入排序），可能會進行n次的比較和交換才能將該資料移至正確位置。而希爾排序會用較大的步長移動資料，所以小資料只需進行少數比較和交換即可到正確位置。

一個更好理解的希爾排序實現：將陣列列在一個表中並對列排序（用插入排序）。重複這過程，不過每次用更長的列來進行。最後整個表就只有一列了。將陣列轉換至表是為了更好地理解這演算法，演算法本身僅僅對原陣列進行排序（通過增加索引的步長，例如是用i += step_size

例如，假設有這樣一組數[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我們以步長為5開始進行排序，我們可以通過將這列表放在有5列的表中來更好地描述演算法，這樣他們就應該看起來是這樣：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然後我們對每列進行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

當我們以單行來讀取資料時我們得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].這時10已經移至正確位置了，然後再以3為步長進行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之後變為：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最後以1步長進行排序（此時就是簡單的插入排序了）。

[編輯]步長序列

步長的選擇是希爾排序的重要部分。只要最終步長為1任何步長序列都可以工作。演算法最開始以一定的步長進行排序。然後會繼續以一定步長進行排序，最終演算法以步長為1進行排序。當步長為1時，演算法變為插入排序，這就保證了資料一定會被排序。

Donald Shell 最初建議步長選擇為並且對步長取半直到步長達到 1。雖然這樣取可以比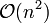類的演算法（插入排序）更好，但這樣仍然有減少平均時間和最差時間的餘地。 可能希爾排序最重要的地方在於當用較小步長排序後，以前用的較大步長仍然是有序的。比如，如果一個數列以步長5進行了排序然後再以步長3進行排序，那麼該數列不僅是以步長3有序，而且是以步長5有序。如果不是這樣，那麼演算法在迭代過程中會打亂以前的順序，那就不會以如此短的時間完成排序了。

步長序列	最壞情況下複雜度

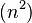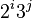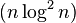已知的最好步長序列由Marcin Ciura設計（1，4，10，23，57，132，301，701，1750，…） 這項研究也表明“比較在希爾排序中是最主要的操作，而不是交換。”用這樣步長序列的希爾排序比插入排序和堆排序都要快，甚至在小陣列中比快速排序還快，但是在涉及大量資料時希爾排序還是比快速排序慢。

另一個在大陣列中表現優異的步長序列是(斐波那契數列除去0和1將剩餘的數以黃金分割比的兩倍的冪進行運算得到的數列)：（1, 9, 34, 182, 836, 4025, 19001, 90358, 428481, 2034035, 9651787, 45806244, 217378076, 1031612713, …）^[2]

[編輯]虛擬碼

input: an array a of length n with array elements numbered 0 to n − 1
inc ← round(n/2)
while inc > 0 do:    
    for i = inc .. n − 1 do:        
        temp ← a[i]        
        j ← i        
        while j ≥ inc and a[j − inc] > temp do:            
            a[j] ← a[j − inc]            
            j ← j − inc        
        a[j] ← temp    
    inc ← round(inc / 2.2)

[編輯]C示例程式碼

#include <stdio.h>
 
int main()
{
     const int n = 5;
     int i, j, temp; 
     int gap = 0;
     int a[] = {5, 4, 3, 2, 1}; 
     while (gap<=n)
     {
          gap = gap * 3 + 1;
     } 
     while (gap > 0) 
     {
         for ( i = gap; i < n; i++ )
         {
             j = i - gap;
             temp = a[i];             
             while (( j >= 0 ) && ( a[j] > temp ))
             {
                 a[j + gap] = a[j];
                 j = j - gap;
             }
             a[j + gap] = temp;
         }
         gap = ( gap - 1 ) / 3;
     }    
 }

[編輯]C++示例程式碼

void shellsort(int *data, size_t size)
{
    for (int gap = size / 2; gap > 0; gap /= 2)
        for (int i = gap; i < size; ++i)
        {
 
             int key = data[i];
             int j = 0;
             for( j = i -gap; j >= 0 && data[j] > key; j -=gap)
             {
                data[j+gap] = data[j];
              }  
             data[j+gap] = key;
         }
}

[編輯]在Java中的示例程式碼

 void shellsort (int[] a, int n)
 {
     int i, j, k, temp, gap;
     int[] gaps = { 1,5,13,43,113,297,815,1989,4711,11969,27901,84801,
                    213331,543749,1355339,3501671,8810089,21521774,
                    58548857,157840433,410151271,1131376761,2147483647 };
     for (k=0; gaps[k]<n; k++) ;
     while (--k >= 0)
     {
         gap = gaps[k];
         for (i=gap; i<n; i++)
         {
             temp = a[i];
             j = i;
             while (j>=gap && a[j-gap]>temp)
             {
                 a[j] = a[j-gap];
                 j = j-gap;
             }
             a[j] = temp;
         }
     }
 }

[編輯]引用