E. Birdstime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Apart from plush toys, Imp is a huge fan of little yellow birds!

To summon birds, Imp needs strong magic. There are n trees in a row on an alley in a park, there is a nest on each of the trees. In the i-th nest there are ci birds; to summon one bird from this nest Imp needs to stay under this tree and it costs him cost

i points of mana. However, for each bird summoned, Imp increases his mana capacity by B points. Imp summons birds one by one, he can summon any number from 0 to ci birds from the i-th nest.

Initially Imp stands under the first tree and has W points of mana, and his mana capacity equals W as well. He can only go forward, and each time he moves from a tree to the next one, he restores X

 points of mana (but it can't exceed his current mana capacity). Moving only forward, what is the maximum number of birds Imp can summon?

Input

The first line contains four integers n, W, B, X (1 ≤ n ≤ 103, 0 ≤ W, B, X ≤ 109) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.

The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) — where ci is the number of birds living in the i-th nest. It is guaranteed that .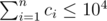

The third line contains n integers cost1, cost2, ..., costn (0 ≤ costi ≤ 109), where costi is the mana cost to summon a bird from the i-th nest.

Output

Print a single integer — the maximum number of birds Imp can summon.

ExamplesinputCopy

2 12 0 4
3 4
4 2

output

6

inputCopy

4 1000 10 35
1 2 4 5
1000 500 250 200

output

5

inputCopy

2 10 7 11
2 10
6 1

output

11

Note

In the first sample base amount of Imp's mana is equal to 12 (with maximum capacity also equal to 12). After he summons two birds from the first nest, he loses 8 mana points, although his maximum capacity will not increase (since B = 0). After this step his mana will be 4 of 12; during the move you will replenish 4 mana points, and hence own 8 mana out of 12 possible. Now it's optimal to take 4 birds from the second nest and spend 8 mana. The final answer will be — 6.

In the second sample the base amount of mana is equal to 1000. The right choice will be to simply pick all birds from the last nest. Note that Imp's mana doesn't restore while moving because it's initially full.

有n棵樹，每棵樹Ci個鳥，買一個花費Costi元。最開始錢包容量和錢數都是w元，且買一個鳥錢包容量增加一個定值。現在按順序從1號樹走到n號樹，每換一棵樹多出來x元，最多買多少鳥？

明顯的一個DP，容易看出現在走到第i棵樹可以作為DP的一維。

看題之後發現，費用數量很大，可能有1e9，顯然費用不能作為DP的一維。而影響買鳥數量的因素，除了費用就是錢包容量了。而且，當鳥的數量一定時，錢包容量是相等的！

由此，我們可以把鳥的數量當做DP的另一維，去找每個對應的DP狀態的剩下的錢最多是多少。

dp[i][j]表示走到第i棵樹下，買了j個鳥剩下的錢數最多是多少，最後只要找dp[n][j]>=0的最大的j，就是答案。

轉移方程：dp[i][j]=max(dp[i-1][j-k]-k*cost[i])，k表示在當前這棵樹上買的鳥數，0<=k<=Ci.

#include <cstdio>
#include <iostream>
#include <string.h>
#include <string> 
#include <map>
#include <queue>
#include <deque>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int maxn=1005,maxk=10005,inf=0x3f3f3f3f;  
const ll llinf=0x3f3f3f3f3f3f3f3f;   
const ld pi=acos(-1.0L);
ll a[maxn],c[maxn];
ll dp[maxn][maxk];

int main() {
	ll n,w,b,x,i,j,k;
	scanf("%I64d%I64d%I64d%I64d",&n,&w,&b,&x);
	for (i=1;i<=n;i++) 
		scanf("%I64d",&a[i]);
	for (i=1;i<=n;i++) 
		scanf("%I64d",&c[i]);
	memset(dp,-1,sizeof(dp));
	dp[0][0]=w;
	ll sum=0;
	for (i=1;i<=n;i++) {
		sum+=a[i];
		ll cap=w;
		for (j=0;j<=sum;j++) {
			for (k=0;k<=a[i]&&k<=j;k++) {
				if (dp[i-1][j-k]==-1) continue;
				if (k*c[i]>dp[i-1][j-k]) continue;
				dp[i][j]=max(dp[i][j],dp[i-1][j-k]-k*c[i]);
			}
			if (dp[i][j]!=-1) dp[i][j]=min(dp[i][j]+x,cap);
			cap+=b;
		}
	}
	ll ans=0;
	for (i=0;i<=sum;i++)
		if (dp[n][i]!=-1) ans=i;
	printf("%I64d\n",ans);
	return 0;
}