OpenJudge 2.5-1700 八皇后問題【回溯演算法】
阿新 • • 發佈:2019-01-04
Description
在國際象棋棋盤上放置八個皇后,要求每兩個皇后之間不能直接吃掉對方。
Input
無輸入。
Output
按給定順序和格式輸出所有八皇后問題的解(見Sample Output)。
Sample Input
Sample Output
若定義一維陣列que[8]表示皇后的位置:第i行皇后放在第j列,用a[i]=j來表示,即下標是行數,內容是列數。
用標誌陣列作為if語句的條件判斷皇后是否可放。
對於某個滿足要求的8皇后的擺放方法,定義一個皇后串a與之對應,即a=b1b2...b8,其中bi為相應擺法中第i行皇后所處的列數。已經知道8皇后問題一共有92組解(即92個不同的皇后串)。
給出一個數b,要求輸出第b個串。串的比較是這樣的:皇后串x置於皇后串y之前,當且僅當將x視為整數時比y小。
Input 第1行是測試資料的組數n,後面跟著n行輸入。每組測試資料佔1行,包括一個正整數b(1 <= b <= 92) Output 輸出有n行,每行輸出對應一個輸入。輸出應是一個正整數,是對應於b的皇后串。 Sample Input
No. 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 No. 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 No. 3 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 No. 4 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 No. 5 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 No. 6 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 No. 7 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 No. 8 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 No. 9 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 ...以下省略
這是一道很經典的回溯題,我們可以通過回溯演算法框架來寫。題目要求在國際象棋棋盤中放置8個皇后使任意兩個皇后都不能互相吃(皇后能吃同一行、同一列、同一對角線的任意棋子)。
分析如下:
很容易想到棋盤上每放一個皇后就標記該行該列以及主對角線和從對角線。用bool陣列md(main diagonal)和cd()標誌兩條對角線。
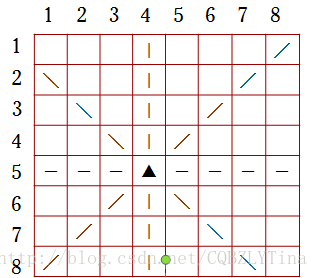
顯然問題在於如何標記某個皇后所在的行、列、對角線上是否有別的皇后;可以從矩陣的特點上找到規律,顯而易見的是:如果在同一行,則行號相同;如果在同一列上,則列號相同;對角線可以通過畫圖找規律探索:在主對角線上的行列值之差相同;從對角線上的行列值之和相同;如下圖(一本通P242 圖5-1):
若定義一維陣列que[8]表示皇后的位置:第i行皇后放在第j列,用a[i]=j來表示,即下標是行數,內容是列數。
用標誌陣列作為if語句的條件判斷皇后是否可放。
演算法思路:
int search(i);
{
int j;//第i個皇后的位置
for (j=1;j<=8;j++ )
if (能放置皇后,即滿足行列及對角線都沒有被標記)
{
放置第i個皇后;
標記標誌陣列;
if (i==8) 輸出 //已經放完個皇后
else search(i+1 - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
還是來看一下程式碼實現:
//2.5 1700 八皇后問題
#include<iostream>
using namespace std;
bool c[9],md[16],cd[16];//標誌陣列,儘量起“望文生義”的名字,好記
int a[9];
int sum=0;//計數
int print();
int search(int i)
{
for(int j=1;j<=8;j++)
if(!c[j]&&!md[i-j+7]&&!cd[i+j])//如果列、對角線上可放
{
a[i]=j;//儲存列號
c[j]=1;
md[i-j+7]=1;
cd[i+j]=1;//標誌“佔領”
if(i==8)
print();//8個皇后都放置好
else search(i+1);//回溯
c[j]=0;
md[i-j+7]=0;
cd[i+j]=0;
}
}
int print()
{
sum++;
cout<<"No. "<<sum<<endl;
for(int j=1;j<=8;j++)
{
for(int i=1;i<=8;i++)
if(a[i]==j)
{ if(i==8)cout<<1;
else cout<<1<<" ";}
else{
if(i==8)cout<<0;
else cout<<0<<" ";
}
cout<<endl;
}
}
int main()
{
search(1);
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
在做這一道題的時候,沒留心樣例,每個方陣中的行列是倒置的,還WA了一次QAQ
另外,輸出方式會有所改變,也可以按自己喜歡的方式來,2.5的1756就是改變了輸出方式:
Description 會下國際象棋的人都很清楚:皇后可以在橫、豎、斜線上不限步數地吃掉其他棋子。如何將8個皇后放在棋盤上(有8 * 8個方格),使它們誰也不能被吃掉!這就是著名的八皇后問題。對於某個滿足要求的8皇后的擺放方法,定義一個皇后串a與之對應,即a=b1b2...b8,其中bi為相應擺法中第i行皇后所處的列數。已經知道8皇后問題一共有92組解(即92個不同的皇后串)。
給出一個數b,要求輸出第b個串。串的比較是這樣的:皇后串x置於皇后串y之前,當且僅當將x視為整數時比y小。
Input 第1行是測試資料的組數n,後面跟著n行輸入。每組測試資料佔1行,包括一個正整數b(1 <= b <= 92) Output 輸出有n行,每行輸出對應一個輸入。輸出應是一個正整數,是對應於b的皇后串。 Sample Input
2 1 92Sample Output
15863724 84136275
怎麼樣,也去試一試吧!