主席樹 (動態)圖文講解讓你一次就懂 zoj2112為例
主席樹(動態)
其實靜態主席樹我們弄清楚之後,動態的可以很快學會。因為動態主席樹就是在靜態主席樹的基礎上增加了一批用樹狀陣列思維維護的線段樹。
我們以下面的例子講解。
5 3
3 2 1 4 7
Q 1 4 3 詢問區間[1,4]第3小數
C 2 6 把第2個數變為6
Q 2 5 3 詢問區間[2,5]第3小數
n是原序列個數
T[i]表示第i棵線段樹的根節點編號
S[i]表示樹狀陣列思維建的第i棵線段樹的根節點編號
L[i]表示節點i的左子節點編號
R[i]表示節點i的右子節點編號
sum[i]表示節點i對應區間中數的個數。
這裡離散化建樹過程和靜態主席樹有一點不同,我們必須把所有詢問先存起來並且把改變的數也加入到原序列中再離散化建樹,會導致空間複雜度和靜態有所區別(之前講靜態的時候提過)。所以這裡我們離散化後序列為3 2 1 4 6 5分別對應原序列的3 2 1 4 7和改變後的6。
之後同靜態一樣建空樹,按原序列字首建樹,相信不用我說了。(畫圖有點麻煩,我借鑑參考部落格的圖,這個圖是沒錯的)

接下來就是重點了,對於題目給出的修改操作,我們新建一批線段樹來記錄更新,這些線段樹以樹狀陣列的思維來維護。
一開始,S[0]、S[1]、S[2]、S[3]、S[4]、S[5] (注意一共有n+1個 即 0到n)(樹狀陣列的每個節點)這些都與T[0]相同(也就是每個節點建了一棵空樹)。
對於C 2 6 這個操作, 我們只需要減去一個2,加上一個5(對應改變後的6)即可。
這個更新我們按樹狀陣列的思想更新,比如這裡的減2,我們要從i=2(原序列中第2個數2在離散化後序列中的位置)即S[2]開始更新,並往上lowbit(i)直到大於5,這裡我們會更新S[2]和S[4]。
邊看圖邊理解(這個圖最後應該是在節點5那裡減1)
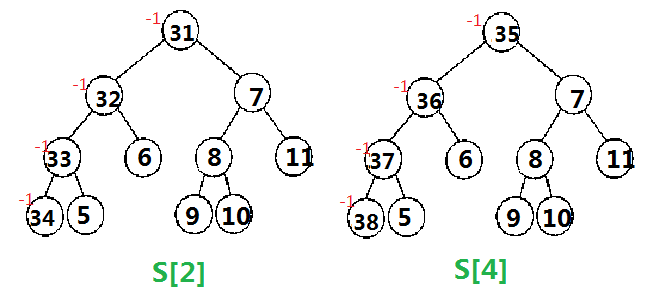
對於加5同樣是從S[2]開始更新
(這個圖最後應該是在節點10那裡加1)
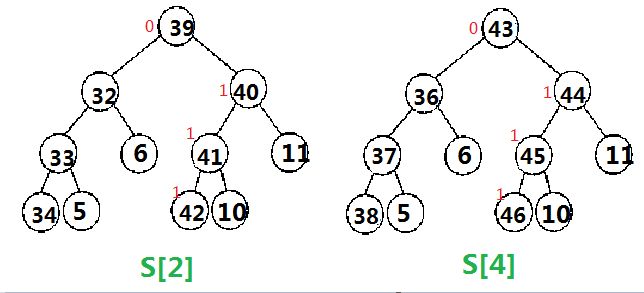
這樣我們查詢的時候T[]和靜態一樣,再按樹狀陣列的思維加上S[]就可算出每個節點對應區間中數的個數,再按靜態的思想查詢即可。
對於原序列n個數,m次詢問
空間複雜度(我的理解)
因為這裡我們要加入詢問中數離散化後再建樹,所以建樹4*(n+m)
按原序列更新T[],n
每次詢問更新S[],2
加起來即可,不過你真這麼開陣列的話肯定會MLE。
以zoj2112為例,參考部落格開的範圍是2*(n+m)
我猜大概是因為如果每次詢問都是修改操作的話按靜態中的開應該會是(n+m)
時間複雜度(我的理解)
m
ZOJ2112
題意
給你n(<=5e4)個數,m(<=1e4)次詢問。
Q i j k 為問區間[i,j]第k小的數
C i t 為把原序列中第i個數變為t
題解
裸題,邊看程式碼邊理解上面思想
#include <bits/stdc++.h>
using namespace std;
const int maxn = 6e4+5;
const int maxm = 1e4+5;
int T[maxn],S[maxn],L[maxn*32],R[maxn*32],sum[maxn*32];
int sz[maxn],h[maxn];
int ul[maxn],ur[maxn];
int tot,num,n,q;
struct node{
int l,r,k;
bool flag; //ture代表Q,false代表C
}Q[maxm]; //儲存詢問
void build(int& rt,int l,int r)
{
rt = ++tot;
sum[rt]=0;
if(l==r) return;
int mid = (l+r)>>1;
build(L[rt],l,mid);
build(R[rt],mid+1,r);
}
void update(int& rt,int pre,int l,int r,int x,int val)
{
rt = ++tot;
L[rt] = L[pre];
R[rt] = R[pre];
sum[rt] = sum[pre]+val;
if(l==r) return;
int mid = (l+r)>>1;
if(x<=mid) update(L[rt],L[pre],l,mid,x,val);
else update(R[rt],R[pre],mid+1,r,x,val);
}
int lowbit(int x)
{
return x&(-x);
}
void add(int x,int val)
{
int res = lower_bound(h+1,h+1+num,sz[x])-h;
while(x<=n)
{
update(S[x],S[x],1,num,res,val);
x += lowbit(x);
}
}
int Sum(int x,bool flag)
{
int res=0;
while(x>0)
{
if(flag) res += sum[L[ur[x]]];
else res += sum[L[ul[x]]];
x -= lowbit(x);
}
return res;
}
int query(int s,int e,int ts,int te,int l,int r,int k)
{
if(l==r) return l;
int mid = (l+r)>>1;
int res = Sum(e,true)-Sum(s,false)+sum[L[te]]-sum[L[ts]];
if(k<=res)
{
for(int i=e;i;i-=lowbit(i)) ur[i] = L[ur[i]];
for(int i=s;i;i-=lowbit(i)) ul[i] = L[ul[i]];
return query(s,e,L[ts],L[te],l,mid,k);
}
else
{
for(int i=e;i;i-=lowbit(i)) ur[i] = R[ur[i]];
for(int i=s;i;i-=lowbit(i)) ul[i] = R[ul[i]];
return query(s,e,R[ts],R[te],mid+1,r,k-res);
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
char str[5];
num=0;
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",sz+i),h[++num]=sz[i];
for(int i=1;i<=q;i++)
{
scanf("%s",str);
if(str[0]=='Q')
{
scanf("%d%d%d",&Q[i].l,&Q[i].r,&Q[i].k);
Q[i].flag=true;
}
else
{
scanf("%d%d",&Q[i].l,&Q[i].r);
Q[i].flag=false;
h[++num]=Q[i].r;
}
}
sort(h+1,h+1+num);
int tmp = unique(h+1,h+1+num)-h-1;
num = tmp;
tot=0;
build(T[0],1,num);
for(int i=1;i<=n;i++) update(T[i],T[i-1],1,num,lower_bound(h+1,h+1+num,sz[i])-h,1);
for(int i=1;i<=n;i++) S[i] = T[0];
for(int i=1;i<=q;i++)
{
if(Q[i].flag)
{
for(int j=Q[i].r;j;j-=lowbit(j)) ur[j] = S[j];
for(int j=Q[i].l-1;j;j-=lowbit(j)) ul[j] = S[j];
printf("%d\n",h[query(Q[i].l-1,Q[i].r,T[Q[i].l-1],T[Q[i].r],1,num,Q[i].k)]);
}
else
{
add(Q[i].l,-1);
sz[Q[i].l] = Q[i].r;
add(Q[i].l,1);
}
}
}
return 0;
}
比較抽象,真不太好通過文字表達清楚,結合程式碼多看幾遍講解應該還是能搞清楚的,切記不要浮躁。
