一篇文章理解矩陣在講什麼。

• 最近在學習矩陣相關知識，但是其抽象的解釋讓人摸不著頭腦，通過瀏覽一些部落格的內容和自己的理解，本文通過通俗的語言將矩陣的內涵做了總結。其中除了書本和個人觀點，部分引用部落格：。本文主要幫助大家理解矩陣，但不一定都是正確的，但願能起到促進學習的作用。

  正式開始之前，我們需要明確一些事情，什麼是問題的實質，什麼是解決問題的工具。比如相似矩陣，相似是一類問題的實質，雖然兩個矩陣相似，但是我們通過矩陣並不能清楚看出他們的特點作用，於是我們引入對角化這個工具，將n階矩陣通過對角化轉成對角矩陣便於運算和理解。本文只講思想，不測重計算，所以舉例皆為3階及以下矩陣。
  

第一節：

矩陣這麼多的應用是有一個前提條件的，那就是這個矩陣是位於線性空間當中的。本節主要講述什麼是線性空間，以及一些基本的規定（概念）。

• 線性空間（又稱向量空間）和子線性空間。
  書本概念:線性空間是滿足……的一個封閉空間。線性子空間是在滿足上述特點的同時還要是父空間（自定義概念，便於理解）的子集。那什麼是線性空間?我們怎麼才能從線性空間中分割一個子線性空間出來呢。舉個很簡單的例子：
  我們以三維空間T為例，它的x,y,z軸座標分別從負無窮到正無窮。根據以往的經驗很顯然，它是一個封閉的空間，而且滿足線性空間的特點，所以它肯定是一個線性空間。現在我去掉它的一個維度，比如讓Z=常數，這時候我們得到一個二維空間S，空間S實際上只包含x,y兩個維度，根據以往的經驗，很容易知道它也是一個線性空間，因此S也是T的子線性空間。同理我們再去掉一個維度，讓空間變成一維空間。這些也是成立的。

• 特殊的向量空間。
  歐式空間：簡單理解為可以用長度角度等來度量的線性空間，帶有內積的空間（內積可以理解為投影，是空間可以度量的一種表現形式，我們通過長度和夾角來求內積，也可以反過來用內積表示長度和大小）高中幾何的空間就是歐式空間。
  酉空間：一種特殊的帶有正定埃爾米特型的復內積空間V（非完備內積空間），可以進行與歐式空間類似的度量，度量工具如：範數（範數：簡單理解為向量的長度，到0點的距離，將向量空間物件進行歐式空間的描述，簡化理解）。
  希爾伯特空間:完備的內積空間。
  完備性：其中完備性的意思就是空間中的極限運算不能跑出該空間，如有理數空間中的√2 的小數表示，其極限隨著小數位數的增加收斂到√2，但√2 屬於無理數，並不在有理數空間。
  關於空間的推導遞進關係可以參考部落格：
  

  http://blog.csdn.net/shijing_0214/article/details/51052208。
  理解：現在我們學習的空間是對我們生活中常用的歐式歐式空間的一個抽象提升，比如距離長度對應抽象提升為範數，角度的表示抽象成內積相關，理解簡化學習難度。

• 空間的維數，基與座標。
  在這門學科中，空間的物體都是由向量或者向量的組合進行表示。在之前的數學中，我們使用的座標系是固定的，為了簡化，我們規定座標系後就忽略了基向量，但現在因為座標系不在固定（個人覺這是因為，矩陣中使用的空間是一種廣義的空間，所有的物體都包含在該空間內，沒有人可以跳出這個空間來規定哪裡是基向量，我們都是處於空間中不同的角度來觀察這個空間，這樣我們必須同時使用所處的相對座標系和相對座標來描述空間的物體，這種空間在某種意義上涵蓋更為廣泛，更加貼近對現實的客觀描述），我們描述一個物體時就要同時表明他的座標系（基向量的組合）和座標。
  基向量相當於每個維度的單位向量，我們用向量或者向量的組合表示的物體可以整理為座標+基向量，例如在基向量x,y,z.構成的空間中，我們有一個點O,我們有三個方向的向量表示該點：a,b,c。那麼我們也可以說是在以x,y,z為基向量的空間中，點O的座標為：(|a|/|x|,|b|/|y|,|c|/|z|)。
  這幾個概念都非常簡單，後面章節有用到的會相應的說明。

第二節

這一節主要講矩陣的線性變換，這些變換是整個線代的基礎重點，弄懂了這些東西的實際物理意義將會大大幫助後面的學習和理解。

什麼是線性變換（這是一種規定性質，很容易理解這裡不做解釋）？線性變換可以用一個矩陣來描述，所以矩陣的本質是一個變換，矩陣的乘法就是將這個變換施加給被乘的物件（可以是單點物件也可以是多點物件，單點對應一個向量，多點對應一個矩陣）。這麼說可能不太具體，你可能還有疑問說，左乘和右乘的結果為啥不一樣？我們舉個簡單的例子來證明這個觀點。
先看一般情況，普通空間中，我們通過旋轉，縮放來描述一個物體的變換。下面是三維空間下的旋轉矩陣，我們可以嘗試將其放在右面去乘一個向量點，我們發現點會繞規定的座標旋轉，但是尺寸沒有發生變化，因為這些旋轉因子的行列式為1，使得旋轉不會影響尺寸的變化。
矩陣在三個方向的旋轉因子：

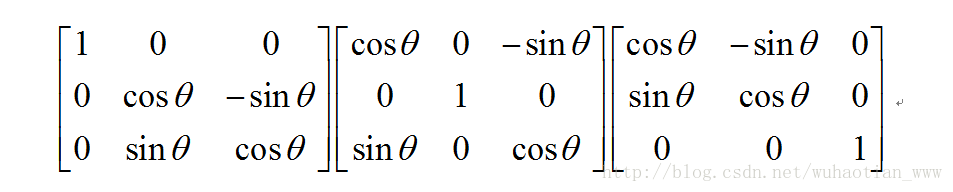
矩陣的縮放因子：

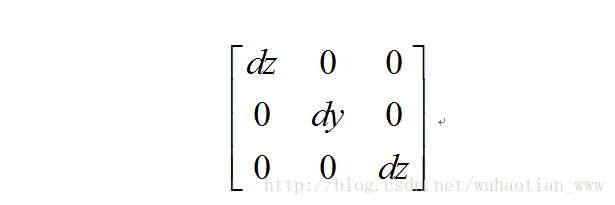
矩陣三個方向的平移因子：

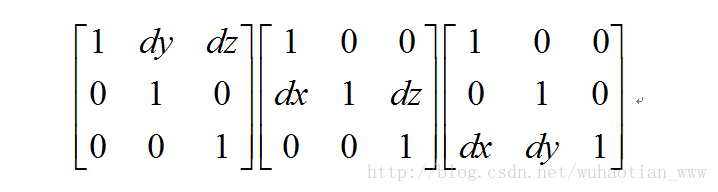
關於這三種變換可以看部落格：http://blog.csdn.net/leaf6094189/article/details/18554549。
說完右乘，我們看一下左乘，由於矩陣運算的特殊性，A*B != B*A。我們引入一個工具來使其相等，這個工具就是轉置。將一個右乘的矩陣公式按照一定規律改變一下位置就可以實現左乘。如下：

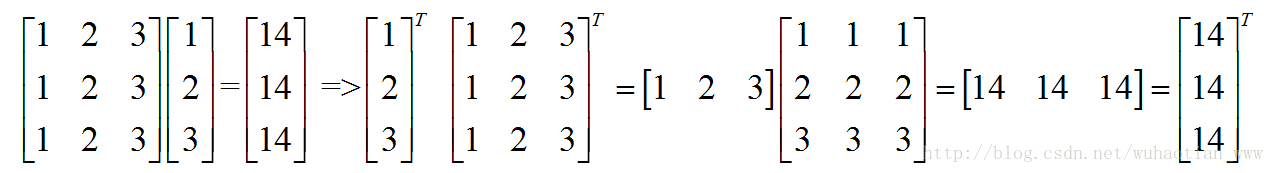
這樣我們就很容易的實現左右乘的轉換。

有了以上對變化的理解，我們還是會有疑問，一個看起來毫無規律的矩陣我們怎麼知道他描述了怎樣的變化？對於一個普通的矩陣我們確實無法直觀的看出它描述了怎樣的變化，我們需要先將普通矩陣進行等價變換（初等變換），然後根據旋轉，縮放，平移的因子矩陣，就可以看出這個矩陣的具體含義。比如對於單純的縮放矩陣，它可以變換成對角矩陣，這樣我們很容易看出它的縮放因子。比如對於單純的平移矩陣，我們可以將它變換成初等矩陣，這樣我們很容易看出它的平移關係。對於旋轉來說變換較為麻煩，但是原理相似，看官可以自行推導。
上面使用了一種變換工具，初等變換。通過上面的例子，相信我們就不難理解，書本上為什麼要花費不少篇幅來講解初等變換和初等矩陣了。

矩陣為什麼支援分塊計算？我們該怎麼分塊。
先從簡單的劃分開始:

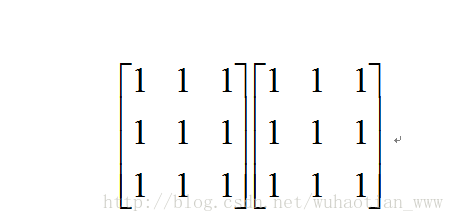
（1）我們把左邊的矩陣當作變換矩陣，那麼右邊的矩陣就相當於待變換點的組合，無論是一個還是兩個都不影響計算結果，所以右邊矩陣的任意行劃分都不影響結果。
（2）我們把右邊的矩陣當作變換矩陣，那麼左邊的矩陣就相當於待變換點的組合，無論是一個還是兩個都不影響計算結果，所以左邊矩陣的任意列劃分都不影響結果。
接下來看左矩陣的列劃分和右矩陣的行劃分。

從網上找了個例題：要想能使用矩陣乘法計算，我們必須把A的列每段劃分的個數與B行每段劃分的個數相同，這個不難理解。現在我們忽略掉矩陣中的0元素，將其當作普通元素處理。那麼我們會得到下面的式子：

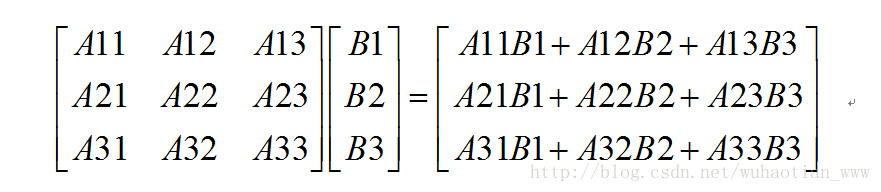
不難看出計算結果和不分塊時完全一樣，只是簡單的拆分組合。究其原因我們可以將其理解為在滿足劃分特點的情況下，分塊計算就相當於對某個或某幾個維度分量進行計算，然後求和的過程。
綜合上面幾條，滿足上面特點的任何劃分都是成立的。

逆矩陣：AA-1 =E;
目前先了解逆矩陣相當於矩陣的倒數，兩者相乘等於單位矩陣。它有很多特點，後面使用到了會繼續解釋，比如非奇異矩陣行列式，|A|=1/|A-1|.等等。如果從倒數的角度出發就很容易理解。

第三節：行列式與秩。

為了描述行列式的意義，我們自己引入一個概念叫做維度積，舉例理解一下，二維維度積表示面積，三維維度積叫做體積，對於高維我們將其抽象為維度積。有了這個概念之後，我們發現，行列式的代數結果表示的正是矩陣向量所圍成的這種維度積。
關於這個的證明是一項不小的工作量，前人已經證明過了，這裡貼出部落格：
http://blog.csdn.net/vernice/article/details/48512203。

由上面的行列式的幾何含義，我們可以推斷出什麼是奇異矩陣，奇異矩陣就是維度積為0的矩陣（方陣），當方陣中向量不全部線性無關時，維度積為0，比如不完全線性相關的二維方陣表示一條直線，它的二維維度積（面積）為0，比如不完全線性相關的三維方陣表示一條直線或一個平面，它的三維維度積（體積）為0。
所以行列式只有對非奇異矩陣成立，且det(A)=1/det(A-1)。A-1就是定義了A的逆變換，是矩陣A的延伸，用於還原A的變換。
求解A-1除了之前的初等變換方法外，我們還可以通過代數餘子式的方式求解。
餘子式：在一個n階行列式D中,把元素aij (i,j=1,2,…..n)所在的行與列劃去後，剩下的(n-1)^2個元素按照原來的次序組成的一個n-1階行列式Mij,稱為元素aij的餘子式。
代數餘子式：餘子式Mij帶上符號(-1)^(i+j)稱為aij的代數餘子式,記作Aij=(-1)^(i+j) Mij。
餘子式相當於某一面的片面維度積，我們按正負將他們運算組合就可以得到實際維度積。

兩種計算過程中需要的矩陣。
伴隨矩陣：A*,每項為矩陣的代數餘子式。伴隨矩陣用來求逆：A-1=A*/|A|。
增廣矩陣：將線性方程組的前後兩個部分寫在一個矩陣中，通過化簡求解或者通過秩來判斷解的個數。這就引入了一個工具秩。
秩：矩陣A的列秩是A的線性獨立的縱列的極大數。通常表示為r(A)，rk(A)或rank A。

相似矩陣：相似矩陣是通過一個變換在不同視角的表現形式，它們的特點相同。我們可以通過計算相似矩陣來簡化運算。B=P-1AP,該公式可以簡單理解為矩陣B與後面三個矩陣的組合效果相同。假設我們有一個向量x，讓x進行B變化，等到在B所在視角下的變換結果。等號右面讓x先做P變換，將座標點變換到A所在的座標系當中，然後對變換點做A變換，然後將變換結果逆變換到B的座標系下。這時我們發現兩個結果相同，顯然很容易理解這個結果。

第四節：特徵值，特徵向量與二次型。

特徵值和特徵向量在機器學習等的演算法中極為常見也十分重要，這裡對他們實際表示的意義和特點做一個簡單的理解。
設T是數域K上的線性空間Vn的線性變換，且對K中某一數a，存在非0向量x屬於Vn，使得Tx=ax成立，則稱a為T特徵值，x為T的屬於a的特徵向量。

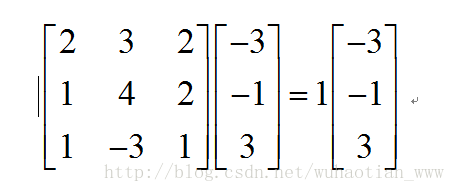
如上式：1為矩陣的特徵值，向量為特徵向量。那麼他們分別代表什麼含義呢。我們知道，矩陣乘法對應了一個變換，是把任意一個向量變成另一個方向或長度都大多不同的新向量。在這個變換的過程中，原向量主要發生旋轉、伸縮的變化。如果矩陣對某一個向量或某些向量只發生伸縮變換，不對這些向量產生旋轉的效果，那麼這些向量就稱為這個矩陣的特徵向量，伸縮的比例就是特徵值。根據之前提到縮放因子，我們知道這個矩陣可以變換成對角陣。但是它對機器學習中的特徵提取有什麼用呢？首先宣告機器學習中的特徵值並不是矩陣論中的特徵值，機器學習中的特徵值是指變化較為顯著，能作為描述一個物體的一個主要特點。當我們有一百個方面來描述一個物體時，我們發現它的計算量十分龐大而且有些方面對結果幾乎不起作用，這時候我們就需要提取出它的主要特徵。目的是讓所有樣本儘量分散，這樣資料資訊就能更充分的表現出來，我們就很容易通過簡單的曲線將資料分類。為了將資料分散，我們先列出所有方面的兩兩協方差矩陣。實對稱矩陣可以化成對角矩陣，而且兩個矩陣相似，通過對角矩陣我們不難發現，經過變換後某些維度的資料資訊較為分散，即對角陣上較大的特徵值，我們將這幾個特徵值選取出來，並提取他們的特徵向量，該向量描述了一種變換，我們將這些方向的變換向量組成一個變換矩陣，然後將原始資料變換到新的空間。該空間的資料就會相對分散，易於分類。
詳細解釋見部落格：http://www.360doc.com/content/13/1124/02/9482_331688889.shtml。

二次型：n個變數的二次多項式稱為二次型，即在一個多項式中，未知數的個數為任意多個，但每一項的次數都為2的多項式。這個概念和我的學習內容不太相關就沒有仔細看，提一下以後用到再回頭學習。

到此終於結束。僅僅記錄一下自己初看矩陣論的想法，肯定是漏洞百出，以後再看肯定會有不同的感悟和見解，以後的感悟以後再做記錄。上面只是將抽象的東西講的便於理解，並沒有嚴謹的證明。所以認真推導和練習是必不可少的。