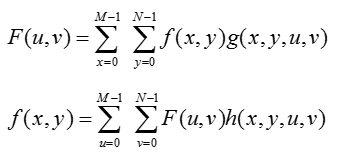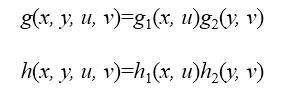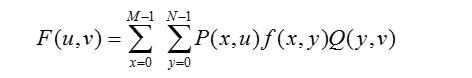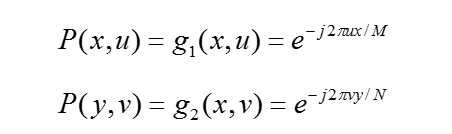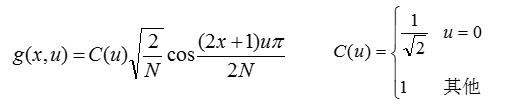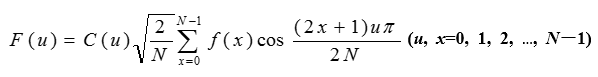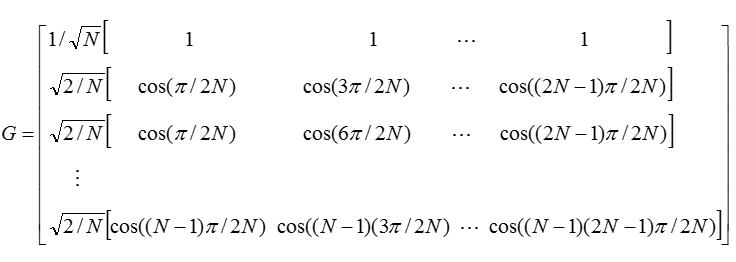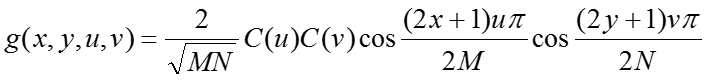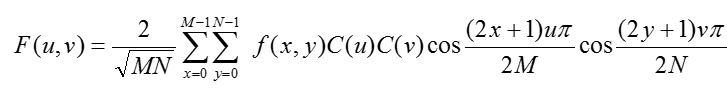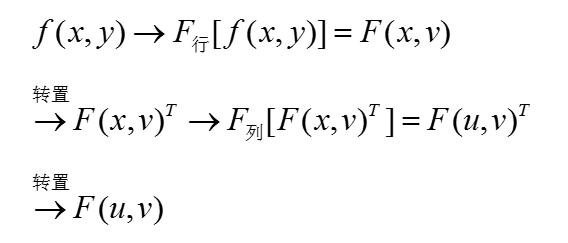1.預備知識

1.1可分離變換

二維傅立葉變換可用通用的關係式來表示：

式中：x, u=0, 1, 2,  …,  M－1；y,  v=0,  1,  2,  …,  N－1；g(x,y,u,v)和h(x,y,u,v)分別稱為正向變換核和反向變換核。  如果滿足 :

則稱正、反變換核是可分離的。進一步，如果g1和g2，h1和h2在函式形式上一樣，則稱該變換核是對稱的。

2.影象變換的矩陣表示

數字影象都是實數矩陣， 設f(x,  y)為M×N的影象灰度矩陣， 通常為了分析、推導方便，可將可分離變換寫成矩陣的形式：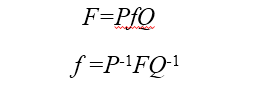                                         

其中，F、f是二維M×N的矩陣；P是M×M矩陣；Q是N×N矩陣。 

式中，u=0,  1,  2,  …,  M－1，v=0,  1,  2,  …,  N－1。
對二維離散傅立葉變換，則有 :

實踐中，除了DFT變換之外，還採用許多其他的可分離的正交變換。例如：離散餘弦變換、沃爾什-哈達瑪變換、K-L變換等。 

2.離散餘弦變換數學原理

離散餘弦變換（Discrete Cosine Transform，DCT）是可分離的變換，其變換核為餘弦函式。DCT除了具有一般的正交變換性質外， 它的變換陣的基向量能很好地描述人類語音訊號和影象訊號的相關特徵。因此，在對語音訊號、影象訊號的變換中，DCT變換被認為是一種準最佳變換。

2.1一維離散餘弦變換定義

一維DCT定義如下： 設{f(x)|x=0,  1,  …,  N-1}為離散的訊號列

看看，這裡我們就用到了特定核函式的可分離性！ 將變換式展開整理後， 可以寫成矩陣的形式， 即 ： F=Gf 

2.2二維離散餘弦變換

二維DCT正變換核為：
式中，x, u=0,  1,  2,  …, M－1； y,  v=0,  1,  2,  …,  N－1。
二維DCT定義如下： 設f(x,  y)為M×N的數字影象矩陣，則 

式中： x,  u=0,  1,  2,  …,  M－1； y,  v=0,  1,  2,  …,  N－1。
通常根據可分離性， 二維DCT可用兩次一維DCT來完成， 其演算法流程與DFT類似， 即 

3.二維DFT與二維DCT的頻譜特徵分析

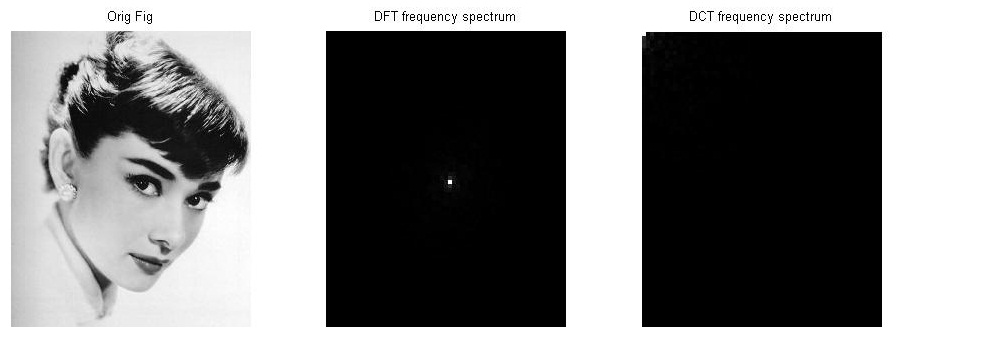
3.1 細節（高頻分量）較少的影象實驗

Conclusion： 對於比較平滑的影象/資料，DFT變換資料集中在中間（低頻訊號區），DCT變換資料集中在左上角，幾乎無法看出DCT的優勢在哪裡。

3.2 細節豐富的影象實驗

Conclusion： DCT變化後的資料很發散，DCT變化後的資料仍然比較集中。如果同樣從頻率譜恢復原始影象，那麼選用DCT更合理，因為DCT只需要儲存更少的資料點。正是這個原因，是的DCT廣泛地應用於影象壓縮。

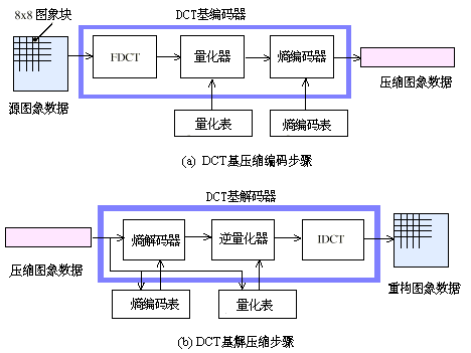
4.DCT應用於影象壓縮

16*16 進行分割槽做DCT變換，然後按照不同的模板進行資料存留與重建。我們會發現，如果儲存的資料過少，會有塊效應現象發生。
64*64的分割槽設定，塊效應更明顯。此時就要在每個分割槽內多采集點資料啦。

6.簡介DCT在JPEG壓縮編碼中的應用

JPEG(Joint Photographic Experts Group) 專家組開發了兩種基本的壓縮演算法，一種是採用以離散餘弦變換(DCT)為基礎的有失真壓縮演算法，另一種是採用以預測技術為基礎的無失真壓縮演算法。使用有失真壓縮演算法時，在壓縮比為25:1的情況下，壓縮後還原得到的影象與原始影象相比較，非影象專家難於找出它們之間的區別，因此得到了廣泛的應用。

JPEG演算法的主要計算步驟

• 正向離散餘弦變換(FDCT)
• 量化(quantization)
• Z字形編碼(zigzag scan)
• 使用差分脈衝編碼調製(differential pulse code modulation，DPCM)對直流係數(DC)進行編碼 
• 使用行程長度編碼(run-length encoding，RLE)對交流係數(AC)進行編碼
• 熵編碼(entropy coding

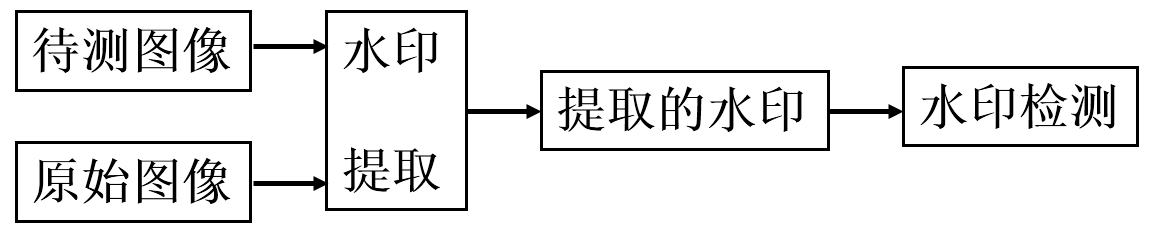
7.DCT在數字水印（digital watermarking）技術中的應用

數字水印技術是將特定的資訊嵌入到數字資訊的內容中,要求嵌入的資訊不能被輕易的去除,在一定的條件下可以被提取出來,以確認作者的版權。 水印嵌入框圖：

水印檢測框圖：