首先，排序演算法的穩定性大家應該都知道，通俗地講就是能保證排序前2個相等的數其在序列的前後位置順序和排序後它們兩個的前後位置順序相同。在簡單形式化一下，如果Ai = Aj，Ai原來在位置前，排序後Ai還是要在Aj位置前。

其次，說一下穩定性的好處。排序演算法如果是穩定的，那麼從一個鍵上排序，然後再從另一個鍵上排序，第一個鍵排序的結果可以為第二個鍵排序所用。基數排序就是這樣，先按低位排序，逐次按高位排序，低位相同的元素其順序再高位也相同時是不會改變的。另外，如果排序演算法穩定，對基於比較的排序演算法而言，元素交換的次數可能會少一些（個人感覺，沒有證實）。

一個班的學生已經按照學號大小排好序了，我現在要求按照年齡從小到大再排個序，如果年齡相同的，必須按照學號從小到大的順序排列。
那麼問題來了，你選擇的年齡排序方法如果是不穩定的，是不是排序完了後年齡相同的一組學生學號就亂了，你就得把這組年齡相同的學生再按照學號拍一遍。
如果是穩定的排序演算法，我就只需要按照年齡排一遍就好了。

這樣看來穩定的排序演算法是不是節省了時間。穩定性的優點就體會出來了。

回到主題，現在分析一下常見的排序演算法的穩定性，每個都給出簡單的理由。

(1)氣泡排序

氣泡排序就是把小的元素往前調或者把大的元素往後調。比較是相鄰的兩個元素比較，交換也發生在這兩個元素之間。所以，如果兩個元素相等，我想你是不會再無聊地把他們倆交換一下的；如果兩個相等的元素沒有相鄰，那麼即使通過前面的兩兩交換把兩個相鄰起來，這時候也不會交換，所以相同元素的前後順序並沒有改變，所以氣泡排序是一種穩定排序演算法。

    //氣泡排序
    public static void bubbleSort(int
 
[] arr){
        for(int i=0;i<arr.length-1;i++){
            for(int j=0;j<arr.length-1-i;j++){
                if(arr[j]>arr[j+1]){
                    arr[j+1]=arr[j]+arr[j+1]-(arr[j]=arr[j+1]);
                }
            }
        }
    }

(2)選擇排序

選擇排序是給每個位置選擇當前元素最小的，比如給第一個位置選擇最小的，在剩餘元素裡面給第二個元素選擇第二小的，依次類推，直到第n - 1個元素，第n個元素不用選擇了，因為只剩下它一個最大的元素了。那麼，在一趟選擇，如果當前元素比一個元素小，而該小的元素又出現在一個和當前元素相等的元素後面，那麼交換後穩定性就被破壞了。比較拗口，舉個例子，序列5 8 5 2 9，我們知道第一遍選擇第1個元素5會和2交換，那麼原序列中2個5的相對前後順序就被破壞了

    //選擇排序1
    public static void selectSort(int[] arr){
        for(int i=0;i<arr.length-1;i++){
            for(int j=i+1;j<arr.length;j++){
                if(arr[i]>arr[j]){
                    arr[i]=arr[i]+arr[j]-(arr[j]=arr[i]);
                }
            }
        }
    }

(3)插入排序

插入排序是在一個已經有序的小序列的基礎上，一次插入一個元素。當然，剛開始這個有序的小序列只有1個元素，就是第一個元素。比較是從有序序列的末尾開始，也就是想要插入的元素和已經有序的最大者開始比起，如果比它大則直接插入在其後面，否則一直往前找直到找到它該插入的位置。如果碰見一個和插入元素相等的，那麼插入元素把想插入的元素放在相等元素的後面。所以，相等元素的前後順序沒有改變，從原無序序列出去的順序就是排好序後的順序，所以插入排序是穩定的。
（12345|5:多次比較後，前面12345已經有序，5不比5小，所以不插到其前）

    //插入排序:1.選取資料2.比較右移3.插入資料
    public static void insertSort(int[] arr){
        int select=0;
        for(int i=1;i<arr.length;i++){
            select=arr[i];
            int j=0;
            for(j=i;j>0&&arr[j-1]>=select;j--){//大小大，變成小大大
                //往前比較，遇到比select大的值，插入到其前
                arr[j]=arr[j-1];//以前的值右移，空出位置給select
            }
            arr[j]=select;
        }
    }

(4)快速排序

以Ai與Aj為例子
快速排序有兩個方向，左邊的i下標一直往右走，當a[i] <= a[center_index]，
其中center_index是中樞元素的陣列下標，一般取為陣列第0個元素。而右邊的
j下標一直往左走，當a[j] > a[center_index]。如果i和j都走不動了，
i <= j, 交換a[i]和a[j],重複上面的過程，直到i>j。
交換a[j]和a[center_index]，完成一趟快速排序。在中樞元素和a[j]交換的
時候，很有可能把前面的元素的穩定性打亂，比如序列5 3 3 4 3 8 9 10 11，
現在中樞元素5和3(第5個元素，下標從1開始計)交換就會把元素3的穩定性打亂
，所以快速排序是一個不穩定的排序演算法，不穩定發生在中樞元素和a[j]交換的時刻。

//快速排序
//核心排序演算法
    public static void sortCore(int[] arr,int startIndex,int endIndex){
        if(startIndex>=endIndex){
            return;
        }

        int boundary=boundary(arr,startIndex,endIndex);

        sortCore(arr,startIndex,boundary);
        sortCore(arr,boundary+1,endIndex);
    }

    //左右兩區部分資料 交換並返回分界點
    private static int boundary(int[] arr, int start, int end) {
        int standard=arr[start];//定義標準，即最左元素
        int leftIndex=start;//左指標
        int rightIndex=end;//右指標

        while(leftIndex<rightIndex){
            while(leftIndex<rightIndex && arr[rightIndex]>=standard){
                rightIndex--; //從右向左查詢
            }
            arr[leftIndex]=arr[rightIndex];//小於基準的移到左端
            //（把第三個3移到最前面）

            while(leftIndex<rightIndex && arr[leftIndex]<=standard){
                leftIndex++;//從左往右查詢
            }
            arr[rightIndex]=arr[leftIndex];//大於基準的移到右端
        }
        arr[leftIndex]=standard;//基準位置不再變化,基準值來到中間
        return leftIndex;
    }

(5)歸併排序

歸併排序是把序列遞迴地分成短序列，遞迴出口是短序列只有1個元素（認為直接有序）或者2個序列（1次比較和交換），然後把各個有序的段序列合併成一個有序的長序列，不斷合併直到原序列全部排好序。可以發現，在1個或2個元素時，1個元素不會交換，2個元素如果大小相等也沒有人故意交換，這不會破壞穩定性。那麼，在短的有序序列合併的過程中，穩定是是否受到破壞？沒有，合併過程中我們可以保證如果兩個當前元素相等時，我們把處在前面的序列的元素儲存在結果序列的前面，這樣就保證了穩定性。所以，歸併排序也是穩定的排序演算法。

如果說穩定性破壞，那隻能是在合併的過程中。
在合併的過程中，2個元素如果相等我們始終會先將左邊子陣列的元素先放入原陣列當中，這樣就不會破壞穩定性
如我們將{1,3,5,3,6,9}排序，在{1,3,5}和{3,6,9}合併的過程中，左邊的元素3先放入陣列中

   //歸併排序
    public static void mergeSort(int[] arr){
        //在排序前，先建好一個長度等於原陣列長度的臨時陣列，避免遞迴中頻繁開闢空間
        int[] temp=new int[arr.length];
        sort(arr,0,arr.length-1,temp);
    }

    public static void sort(int[] arr,int left,int right,int[] temp){
        if(left<right){
            int mid=(left+right)/2;
            sort(arr,left,mid,temp);//左邊歸併排序，使得左子序列有序
            sort(arr,mid+1,right,temp);//右邊歸併排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//將兩個有序子數組合並操作
        }
    }

    public static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i=left;//左序列指標
        int j=mid+1;//右序列指標
        int t=0;
        while(i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++]=arr[i++];
            }else{
                temp[t++]=arr[j++];
            }
        }

        while(i<=mid){//將左邊剩餘元素填充進temp中
            temp[t++]=arr[i++];
        }
        while(j<=right){//將右邊剩餘元素填充進temp中
            temp[t++]=arr[j++];
        }
        t=0;
        //將temp中的元素全部拷貝到原陣列中
        while(left<=right){
            arr[left++]=temp[t++];
        }
    }

(6)基數排序

基數排序是按照低位先排序，然後收集；再按照高位排序，然後再收集；依次類推，直到最高位。有時候有些屬性是有優先順序順序的，先按低優先順序排序，再按高優先順序排序，最後的次序就是高優先順序高的在前，高優先順序相同的低優先順序高的在前。基數排序基於分別排序，分別收集，所以其是穩定的排序演算法。

    //基數排序
    /** 
     * @param arr 待排序陣列 
     * @param radix 基數（10，盒子個數） 
     * @param d 待排序中，最大的位數 
     * */  
    public static void radixSort(int[] arr,int radix,int d){
        int length=arr.length;
        int[] temp=new int[length];//用於暫存元素
        int[] count=new int[radix];//用於記錄待排序元素的資訊,用來表示該位是i的數的個數 
        int divide=1;

        for(int i=0;i<d;i++){
            //重置count陣列，開始統計下一個關鍵字  
            Arrays.fill(count,0);
            //將arr中的元素完全複製到temp陣列中
            System.arraycopy(arr,0,temp,0,length);

            //計算每個待排序資料的子關鍵字
            for(int j=0;j<arr.length;j++){
                int subKey=(temp[j]/divide)%radix;
                count[subKey]++;
            }

            //統計count陣列的前j位（包含j）共有多少個數
            for(int j=1;j<radix;j++){
                count[j]=count[j]+count[j-1];
            }

            //按子關鍵字對指定的資料進行排序，因為開始是從前往後放，現在從後往前讀取，保證基數排序的穩定性
            for(int j=arr.length-1;j>=0;j--){
                int subKey=(temp[j]/divide)%radix;
                count[subKey]--;    
                arr[count[subKey]] = temp[j]; 
              //插入到第--count[subKey]位，因為陣列下標從0開始
            }

            divide = divide * radix; // 1 10 100    
        }       
    }

(7)希爾排序(shell)

希爾排序是按照不同步長對元素進行插入排序，當剛開始元素很無序的時候，步長最大，所以插入排序的元素個數很少，速度很快；當元素基本有序了，步長很小， 插入排序對於有序的序列效率很高。所以，希爾排序的時間複雜度會比O(n^2)好一些。由於多次插入排序，我們知道一次插入排序是穩定的，不會改變相同元素的相對順序，但在不同的插入排序過程中，相同的元素可能在各自的插入排序中移動，最後其穩定性就會被打亂，所以shell排序是不穩定的。

    //希爾排序
    public static void shellSort1(int[] arr){
        //增量gap，並逐漸縮小增量
        for(int gap=arr.length/2;gap>0;gap/=2){
            //從第gap個元素，逐個對其所在組進行直接插入排序操作
            for(int i=gap;i<arr.length;i++){
                int j=i;
                while(j-gap>=0 && arr[j]<arr[j-gap]){
                     //插入排序採用交換法
                    swap(arr,j,j-gap);
                    j-=gap;
                }
            }
        }
    }

(8)堆排序

我們知道堆的結構是節點i的孩子為2 * i和2 * i + 1節點，大頂堆要求父節點大於等於其2個子節點，小頂堆要求父節點小於等於其2個子節點。在一個長為n 的序列，堆排序的過程是從第n / 2開始和其子節點共3個值選擇最大（大頂堆）或者最小（小頂堆），這3個元素之間的選擇當然不會破壞穩定性。但當為n / 2 - 1， n / 2 - 2， … 1這些個父節點選擇元素時，就會破壞穩定性。有可能第n / 2個父節點交換把後面一個元素交換過去了，而第n / 2 - 1個父節點把後面一個相同的元素沒 有交換，那麼這2個相同的元素之間的穩定性就被破壞了。所以，堆排序不是穩定的排序演算法。

    //堆排序
    public static void heapSort(int[] arr){
        //1.構建大頂堆
        for(int i=arr.length/2-1;i>=0;i--){
            //從第一個非葉子節點從下至上、從右至左調整結構
             adjustHeap(arr, i, arr.length - 1);
        }
        //2.調整堆結構，交換堆頂元素和末尾元素
        for(int j=arr.length-1;j>0;j--){
            swap(arr,0,j);//將堆頂元素與末尾元素進行交換
            adjustHeap(arr,0,j);//重新對堆進行調整
        }
    }
    //調整大頂堆（此時大頂堆已構建完成）
    private static void adjustHeap(int[] arr, int i, int end) {
        int temp=arr[i];//取出當前元素
        for(int k=i*2+1;k<=end;k=k*2+1){
            //從i結點的左子節點開始，也就是2*i+1
            if(k+1<=end && arr[k]<arr[k+1]){
                //如果左子節點<右子節點，k指向右子節點
                k++;
            }
            if(arr[k]>temp){
                //如果子節點＞父節點，將子節點值賦給父節點
                arr[i]=arr[k];
                i=k;    
            }else{
                break;
            }       
        }
        arr[i]=temp;//將temp值放到最終的位置
    }

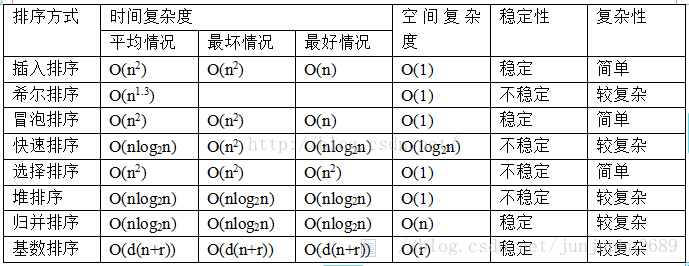
綜上，得出結論:

不穩定：選擇排序、快速排序、希爾排序、堆排序
穩定：氣泡排序、插入排序、歸併排序和基數排序

關於排序方法的選擇：

• (1)若n較小(如n≤50)，可採用直接插入或直接選擇排序。
• 當記錄規模較小時，直接插入排序較好；否則因為直接選擇移動的記錄數少於直接插人，應選直接選擇排序為宜。
• (2)若檔案初始狀態基本有序(指正序)，則應選用直接插入、冒泡或隨機的快速排序為宜；
• (3)若n較大，則應採用時間複雜度為O(nlgn)的排序方法：快速排序、堆排序或歸併排序。