小學生都能看懂的表示式計算(圖解)
基礎知識
會加減乘除(納尼,這個還有不會的嗎)
會雙向連結串列和樹(納尼,還個還要會嗎)
溫故知新
表示式 2 + 3 - 4 + 5,人類計算的過程是這樣的,如下圖:

因為加減操作符優先順序相同,所以從左到右依次運算。
可計算機不會這樣啊,必須先轉化為一棵樹(AST,抽象語法樹,這是編譯原理中的概念)才行,如下圖:

操作符上提變為根節點,左右運算元下降變為葉子節點,它們整體又成了一個運算元。依次對每個操作符使用這個規則,表示式即可變成一棵樹。
再接再厲
表示式 2 + 3 × 4 - 5 ÷ 6,人類的計算過程是這樣的,如下圖:
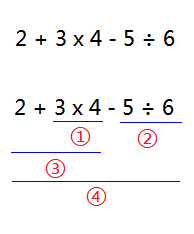
按照優先順序從高到低,先乘除,再加減。
要想讓計算機來算啊,還得先轉換為一棵AST才行,如下圖:
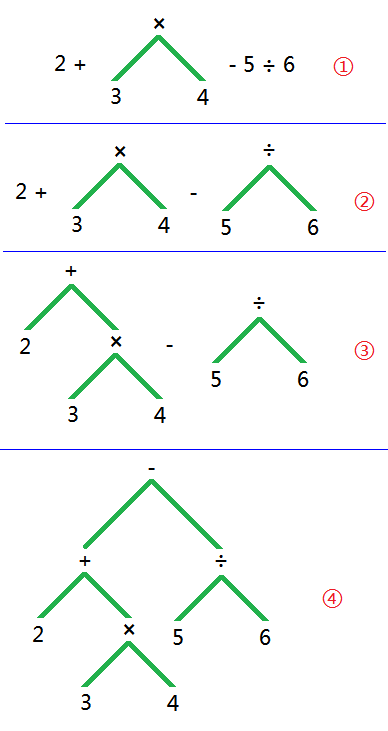
發現問題
綜上,不難發現,先要把一個表示式轉化為一棵AST。人類根據操作符的優先順序很自然地把一個表示式轉化為一棵樹,但是計算機該怎麼做呢?
模仿人類
人類的視線可以在表示式上隨意掃描,對於不復雜的,一眼就發現優先順序高的操作符,瞬間拿到它兩邊的運算元,就可以進行轉化了。
計算機在方式上無法和人類相比,但是在結果上必須要相同,即也要找到優先順序高的操作符,也要知道它兩邊的運算元,然後再進行轉化。
迴歸程式
定義一下操作符的優先順序,優先順序的數值沒有要求,如下圖:
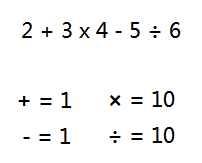
當我們拿到一個操作符時,也要能拿到它左右兩邊的運算元,因操作符和運算元是間隔互聯的,實際它們就是一個雙向連結串列。
因我們要找出優先順序高的操作符,所以必須先找出所有的操作符,然後再判斷優先順序的高低。
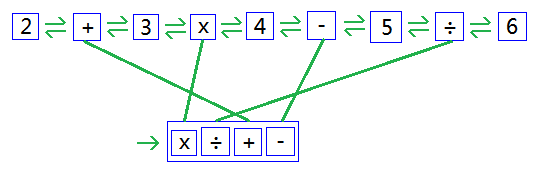
把整個表示式裡的運算元和操作符用雙向連結串列串起來,並把所有的操作符放入一個列表裡。如下圖:

按優先順序從高到低對操作符列表排序,優先順序高的前移,優先順序低的後移,優先順序相同的相對位置不變。如下圖:
取出排在第一位的×,去雙向連結串列裡找出它的左右運算元3和4,把這三個節點轉化為一棵樹,再把該樹作為運算元替換掉原來的三個節點,同時修復好與前面 + 號和後面 - 號的雙向連結。如下圖:
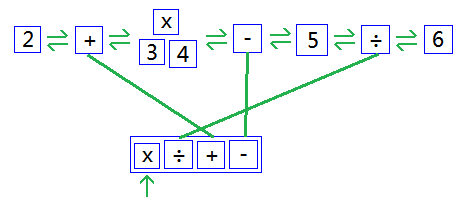
取出第二位的÷,採用和上面相同的方式進行轉化。如下圖:
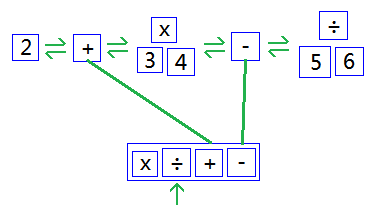
取出第三位的+,採用相同的方式轉化。如下圖:
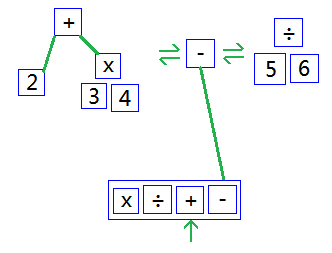
取出最後一位的-,採用相同的方式轉化後,整個表示式轉化完畢,變為一棵AST。如下圖:
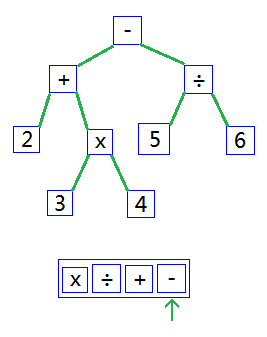
推而廣之
操作符有了優先順序之後,就限制了表示式的計算順序,人們有時希望打破這種限制,就引入了更神奇的操作符,就是小括號啦(哈哈)。
表示式 ( 2 + 3 ) × ( ( 4 - 5 ) ÷ 6 ),如果還想採用上面的套路,那麼核心問題就落到了操作符的優先順序上了。即如何真實地反映每個操作符的優先順序值。
此時我們意識到,操作符的優先順序不再是固定的,而是會隨著有沒有括號以及括號的巢狀深度而變化。其實小括號本來就是改變了操作符的優先順序嘛,我們人類明白這一點,關鍵也要讓計算機明白。
既然括號是操作符,那也為它定義一個優先順序值,這個值最好稍微大一些。如下圖:
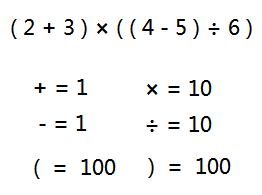
定義一個上下文的基礎優先順序值,預設當然是0了。
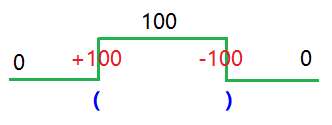
當遇到左括號時,基礎優先順序值加上括號優先順序值,相當於基礎優先順序值得到了提升,這樣括號裡的操作符因為有基礎優先順序值的存在,所以自然擡高了自己的優先順序值(相等於站到了巨人的肩膀上)。
當遇到右括號時,基礎優先順序值減去括號優先順序值,相當於此時新的基礎優先順序值降到了進入括號前的水準。如下圖:
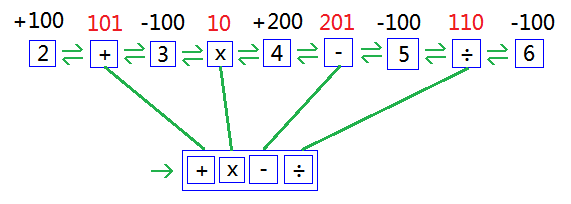
解析表示式,同時計算出每個操作符的優先順序值(牢記,遇到一個左括號加100,遇到一個右括號減100)。如下圖:
按照實際優先順序值從高到低排序操作符列表。如下圖:

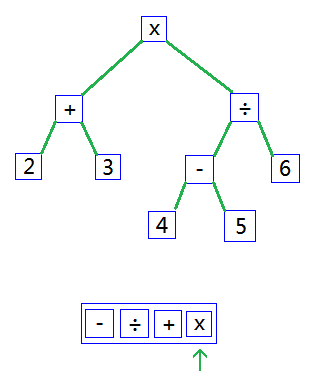
最後按照相同的方式,轉換為一棵AST。如下圖:
後記:人類社會存在的歷史要比計算機的歷史長的多,從人類社會尋找問題的解決思路有時也是一個不錯的方向。甚至可以從大自然中尋找。
(完)
程式設計新說
用獨特的視角說技術

