一、選擇排序

1、演算法原理

每一趟從待排序的記錄當中選出最小的元素，順序放在已經排好序的序列的後面，直到全部記錄排序完畢。

2、演算法思想

首先找到所有數中最小值的下標；找到最小值的下標與第一個位置的數值交換位置，這樣每一次找到的最小值固定在前面；迴圈操作直到遍歷找到所有。

舞蹈之選擇排序：http：//v.youku.com/v_show/id_XMzMyODk5MDI0.html？from = s1.8-1-1.2

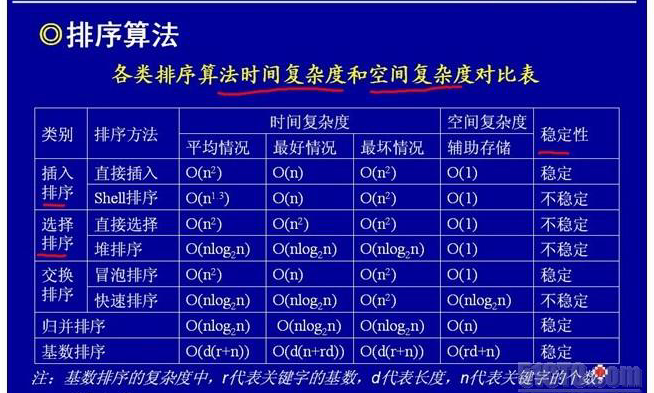
時間複雜度：O（n  ^ 2），由於選擇排序每一輪只交換一次，所以其實際效能要優於氣泡排序。

程式碼演示：

 public static void selectSort(int[] arr){
        for(int i=0;i<arr.length;i++){
            int min=i;
            int j=i+1;
            for(;j<arr.length;j++){
                if(arr[min] > arr[j]){//找出最小值的下標
                  min=j;
                }
            }
            if(min>i) {//將最小值從頭開始放
                int temp = arr[i];
                arr[i] = arr[min];
                arr[min] = temp;
            }
        }
    }
 

二、堆排序

堆排序是一種樹形選擇排序，是對直接選擇排序的有效改進。

1、堆的概念

堆是一顆順序儲存的完全二叉樹。完全二叉樹中所有的非終端結點的值均不大於（均不小於）其左、右孩子結點的值。

小根堆：每個節點的值小於等於其左、右孩子結點的值。

大根堆：每個節點的值大於等於其左、右孩子結點的值。

2、演算法思想

將待排序的序列構造成一個大根堆，此時，整個序列中的最大值就是堆頂的根節點，將其與末尾的元素進行交換，此時，末尾就是最大值，然後將剩餘n-1個元素重新構造成一個堆，這樣得到n個元素的次小值，如此反覆進行執行，就能夠得到一個有序的序列了。

時間複雜度：O（nlong2n）                                                           空間複雜度：O（1）

3、演算法步驟

步驟一：構建初始堆。將給定的無序的序列構造成一個大頂堆（一般升序採用大頂堆，降序採用小頂堆）

此時，我們就將無序陣列構造成了一個大頂堆。

步驟二：將堆頂元素和末尾的元素進行交換，使得末尾的元素最大，然後繼續調整堆，再將堆頂元素和末尾的元素進行交換，得到第二大元素。如此反覆進行交換、重建、交換。

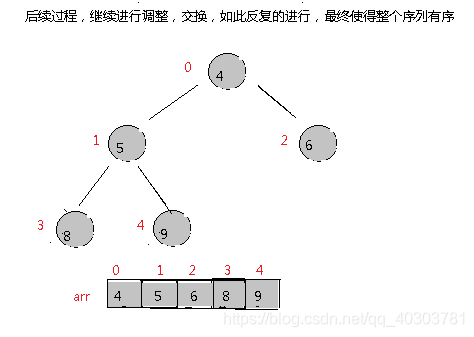
程式碼演示：

public static void adjust(int[] arr, int start, int end) {
        int temp=arr[start];
        for(int i=2*start+1;i<=end;i=2*i+1){
            if(i+1<=end && arr[i]<arr[i+1]){
                i++;//i儲存左右結點的較大值的下標
            }
            if(temp<arr[i]){
                arr[start]=arr[i];
                start=i;
            }else{
                break;
            }
        }
        arr[start]=temp;
    }
    public static void heapSort(int[] arr){
        int i=0;
        for(i=(arr.length-1-1)/2;i>=0;i--){//i代表要調整的根節點的下標
            adjust(arr,i,arr.length-1);//建立最大堆
        }
        int temp=0;
        for(i=0;i<arr.length;i++){
            temp=arr[0];//根儲存最大值
            arr[0]=arr[arr.length-i-1];//arr[0]賦值為當前待排序的最後一個值
            arr[arr.length-1-i]=temp;
            adjust(arr,0,arr.length-1-i-1);
        }
    }
 

三、歸併排序

1、演算法原理

對於給定的一組記錄，利用遞迴和分治技術將資料序列劃分成為越來越小的半子表，再對半子表進行排序，最後再用遞迴的方法將排好序的半子表合併成為有序序列。

舞蹈之歸併排序：http：//v.youku.com/v_show/id_XMzMyODk5Njg4.html？from = s1.8-1-1.2

2、演算法思想

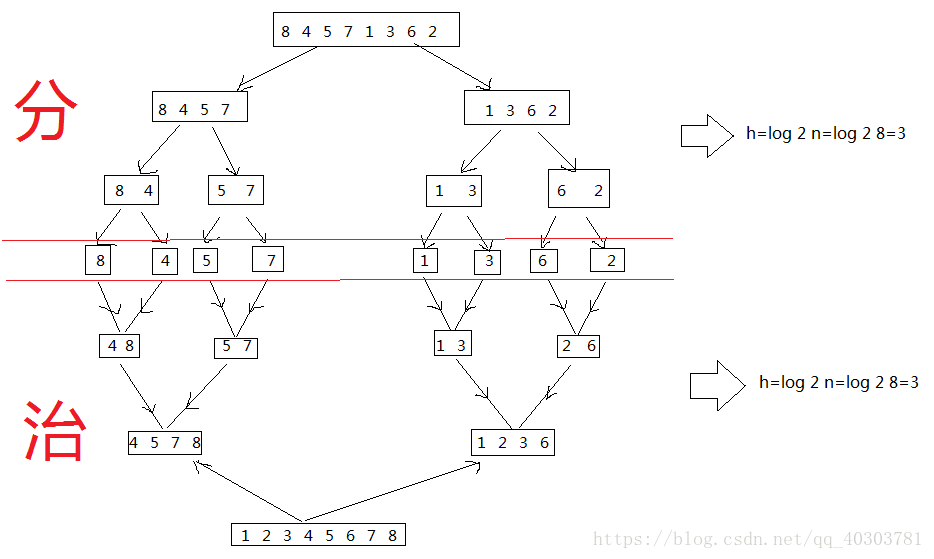
將資料集合兩分拆開；迴圈拆分至每組只剩一個為止；將拆分的陣列進行排序組合；兩兩合併，直至合併成為一個數組。

具體的過程示意如下圖：

程式碼演示：

      public static void mergeSort(int[] arr,int low,int mid,int high) {
          int i=low;
          int j=mid+1;

          int[] temp=new int[high-low+1];
          int k=0;

          while(i<=mid && j<=high){
              if(arr[i]<arr[j]){
                  temp[k++]=arr[i++];
              }else if(arr[i]>arr[j]){
                  temp[k++]=arr[j++];
              }
          }
          while(i<=mid){
              temp[k++]=arr[i++];
          }
          while(j<=high){
              temp[k++]=arr[j++];
          }
          for(int k2=0;k2<temp.length;k2++){
              arr[k2+low]=temp[k2];
          }
      }
      public static void merge(int[] arr,int low,int high){
          int mid=(low+high)/2;
          if(low<high){
              merge(arr,low,mid);
              merge(arr,mid+1,high);

              mergeSort(arr,low,mid,high);
          }
      }