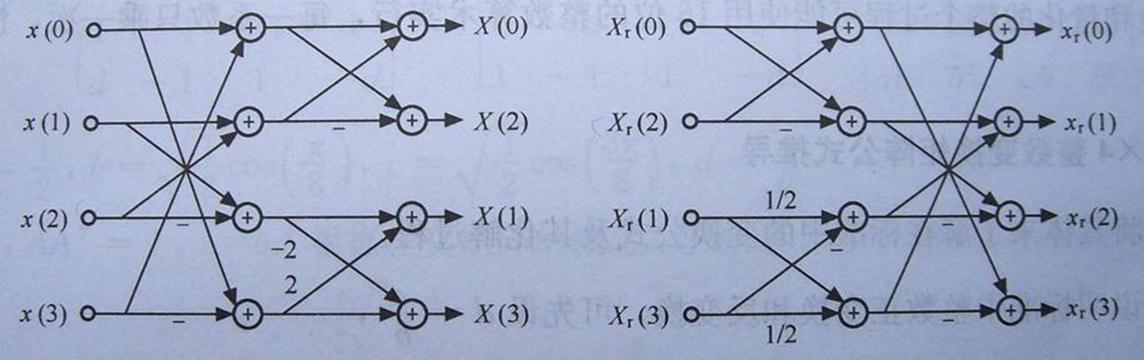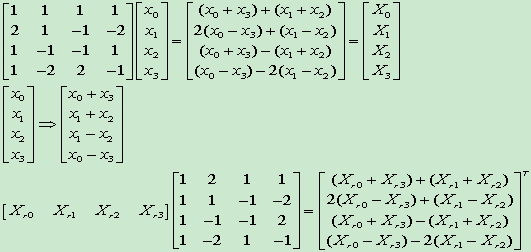H264編碼器6( H.264整數DCT公式推導及蝶形演算法分析)
來自:https://www.cnblogs.com/xkfz007/archive/2012/07/31/2616791.html
這是網上的一篇文章, 我重新讀了一下, 然後做了一些整理
1.為什麼要進行變換
空間影象資料通常是很難壓縮的:相鄰的取樣點具有很強的相關性(相互關聯的),而且能量一般平均分佈在一幅影象中,從而要想丟掉某些資料和降低資料精度而不明顯影響影象質量,就要選擇合適的變換,方法,使影象易於被壓縮。適合壓縮的變換方法要有這樣幾個性質:
(1).可以聚集影象的能量(將能量集中到少數有意義的數值上),如下圖:
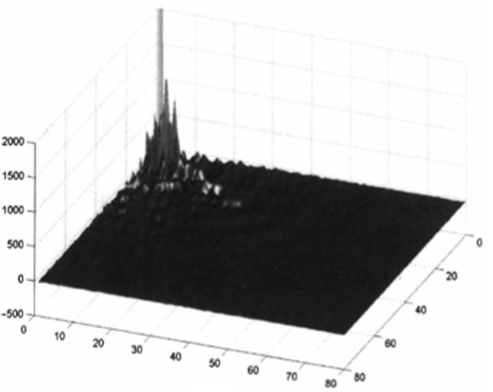
舉個例子說明, 左圖是變換前的資料, 右圖是變換後的資料:
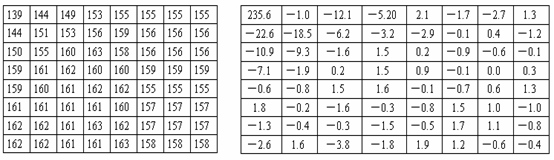
可以看出,經變換後,資料的能量基本上集中到左上方(低頻訊號)了,而變換後的資料完全可以通過反變換還原成原來的資料。為了達到壓縮檔案的目的,我們就可以丟棄掉一些能量低的資料(高頻訊號),而對影象質量影響很小。
- 可以除去資料之間的相關性(以使丟掉不重要的資料對影象的質量影響很少)。
- 變換方法應該適合用軟硬體實現。
2.具體變換過程
4x4的DCT變換矩陣如下:
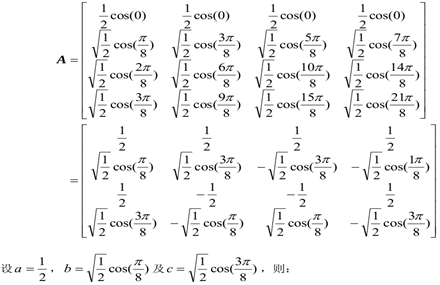
這樣我們就得到了,如下矩陣:
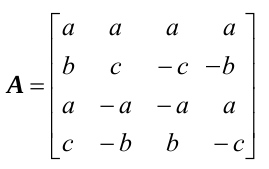
進行推導得到如下:
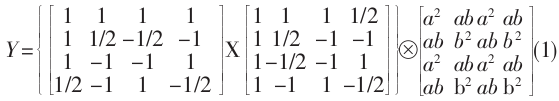
在上式中, 雖然乘以 1/2 的操作可以用右移來實現 , 但這樣會產生截斷誤差 . 因此, 將1/2提到矩陣外面, 並與右邊的點乘合併, 進而得到如下的算式:
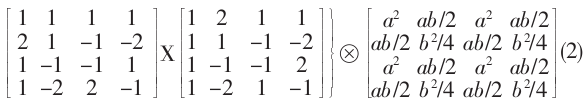
在JM編碼器中,變換過程只包括了
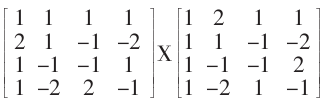
後面的點乘實際上是在量化過程中進行,因為後面的點乘還有實數運算,實數運算將不可避免地產生精度誤差,而且運算量巨大。而量化本身就會丟失一些訊號,因些,這些實數運算放在量化過程中將大大的降低變換的運算率同時又不明顯影響精度?
然而,4X4的矩陣運算如果按常規演算法的話仍要進行64(4*16=64每個點需要4次乘法)次乘法運算和48(3*16=48每個點需要3次乘法)次加法,這將耗費較多的時間,於是在H.264中,有一種改進的 演算法(蝶形演算法)可以減少運算的次數。這種矩陣運算演算法構造非常巧妙,利用構造的矩陣的整數性質和對稱性,可完全將乘法運算轉化為加法運算.
這裡來分析一下蝶形演算法,這個蝶形演算法和一般FFT的蝶形演算法不同,由於我沒有找到相關論文,能找到的書和網路資料又語焉不詳,只好自己推導。上面的JM程式碼就是計算下面三個4x4矩陣的過程。
分析一下前兩個矩陣的乘法,只分析他們結果矩陣的第一列。有什麼辦法可以減少運算量呢?首先採用傳統方法計算,得到結果:
X[0] = x[00]+x[10]+x[20]+x[30]
X[1] = 2*x[00]+x[10]-x[20]-2*x[30]
X[2]= x[00]-x[10]-x[20]+x[30]
X[3] = x[00]-2x[10]+2x[20]-x[30]
計算代價是16次乘法12次加法,考慮到矩陣的1的乘法可以省略,去除8個乘1,還需要8次乘法和12次加法。那麼我們再仔細思考他們的相 關性,從一般演算法意義上來說,可以用空間代價換時間代價,比如設定中間變數來減少計算次數。用不同的顏色把需要重複運算的部分標上,作為中間變數。

那麼提取出來的中間變數將是:
x[00]+x[30]
x[00]-x[30]
x[10]+x[20]
x[10]-x[20]
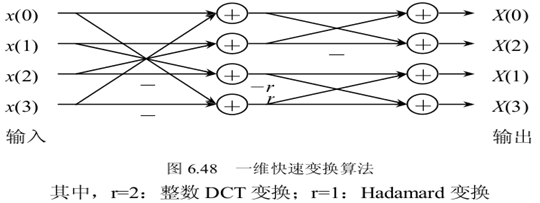
儲存了這四個中間變數,我們對比看看蝶形圖,和圖中第一層的算式相符合。用這些中間變數來組合,就可以把最終的X[0]..X[3], 計算出來。這樣,就把運算量降低到2個乘法和8個加法,剩餘的運算就是疊代這個演算法。
所以,可以得出以下結論:
- 這個蝶形圖和一般意義的FFT或FDCT蝶形圖不同,是對H.264在整數DCT基礎上的具體演算法優化,只對於以上Cf矩陣。
- 計算過程是把上面的三個4x4矩陣乘法分成兩兩矩陣相乘。再把殘差矩陣和後來的中間結果Cf x X一行行分別輸入蝶形圖進行一維整數DCT計算。
- 蝶形圖優化思想就是提取矩陣的相關部分,定義中間變數,減少運算次數。
在JM8.6程式碼中這個碟形演算法, 出現的地方很多, 只要牽扯到變換, 就有這種演算法. 包括Hadamard變換. 在多個函式中出現, 其實現是一樣的.
// Horizontal transform水平變換,其實就是左乘Cf,
for (j=0; j < BLOCK_SIZE && !lossless_qpprime; j++)
{
for (i=0; i < 2; i++)
{
i1=3-i;
m5[i]=img->m7[i][j]+img->m7[i1][j];
m5[i1]=img->m7[i][j]-img->m7[i1][j];
}
img->m7[0][j]=(m5[0]+m5[1]);
img->m7[2][j]=(m5[0]-m5[1]);
img->m7[1][j]=m5[3]*2+m5[2];
img->m7[3][j]=m5[3]-m5[2]*2;
}
// Vertical transform垂直變換,其實就是右乘CfT
for (i=0; i < BLOCK_SIZE && !lossless_qpprime; i++)
{
for (j=0; j < 2; j++)
{
j1=3-j;
m5[j]=img->m7[i][j]+img->m7[i][j1];
m5[j1]=img->m7[i][j]-img->m7[i][j1];
}
img->m7[i][0]=(m5[0]+m5[1]);
img->m7[i][2]=(m5[0]-m5[1]);
img->m7[i][1]=m5[3]*2+m5[2];
img->m7[i][3]=m5[3]-m5[2]*2;
}