深層學習為何要“Deep”（下）

阿新 • • 發佈：2019-01-04

雖然在gitbook上已有為何深層學習，但還是發一下照顧那些關注了超智慧體，又只希望在知乎上看文章的小夥伴。近期由於期刊論文deadline將至（Winter is Coming），變體神經網路（RNN，CNN等不同變體的統一理解）部分會在17號開始繼續寫。

為何深層學習

深層學習開啟了人工智慧的新時代。不論任何行業都害怕錯過這一時代浪潮，因而大批資金和人才爭相湧入。但深層學習卻以“黑箱”而聞名，不僅調參難，訓練難，“新型”網路結構的論文又如雨後春筍般地湧現，使得對所有結構的掌握變成了不現實。我們缺少一個對深層學習合理的認識。

神經網路並不缺少新結構，但缺少一個該領域的 $E=mc^2$

很多人在做神經網路的實驗時會發現調節某些方式和結構會產生意想不到的結果。但就我個人而言，這些發現並不會讓我感到滿足。我更關心這些新發現到底告訴我們了什麼，造成這些現象的背後原因是什麼。我會更想要將新的網路結構歸納到已有的體系當中。這也是我更多思考“為何深層學習有效”的原因。下面便是目前YJango關於這方面的見解。

深層神經網路相比一般的統計學習擁有從數學的嚴謹中不會得出的關於物理世界的先驗知識（非貝葉斯先驗）。該內容也在Bengio大神的論文和演講中多次強調。大神也在Bay Area Deep Learning School 2016的Founda’ons and Challenges of Deep Learning pdf（這裡也有視訊，需翻牆）中提到的distributed representations和compositionality兩點就是神經網路和深層神經網路高效的原因（若有時間，強烈建議看完演講再看該文）。雖然與大神的思考起點可能不同，但結論完全一致（看到Bengio大神的視訊時特別興奮）。下面就是結合例子分析：
1. 為什麼神經網路高效
2. 學習的本質是什麼
3. 為什麼深層神經網路比淺層神經網路更高效
4. 神經網路在什麼問題上不具備優勢

其他推薦讀物

Bengio Y. Learning deep architectures for AI[J]. Foundations and trends® in Machine Learning, 2009, 2(1): 1-127.
Brahma P P, Wu D, She Y. Why Deep Learning Works: A Manifold Disentanglement Perspective[J]. 2015.
Lin H W, Tegmark M. Why does deep and cheap learning work so well?[J]. arXiv preprint arXiv:1608.08225, 2016.

Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(8): 1798-1828.

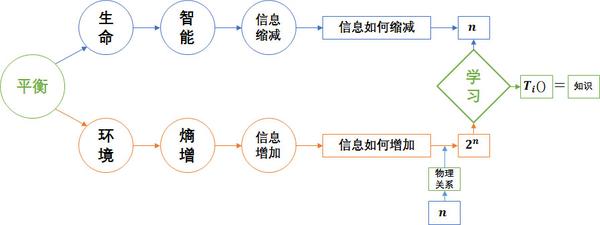
YJango的整個思考流程都圍繞減熵二字進行。之前在《熵與生命》和《生物學習》中討論過，生物要做的是降低環境的熵，將不確定狀態變為確定狀態。通常機器學習是優化損失函式，並用概率來衡量模型優劣。然而概率正是由於無法確定狀態才不得不用的衡量手段。生物真正想要的是沒有絲毫不確定性。

深層神經網路在自然問題上更具優勢，因為它和生物學習一樣，是找回使熵增加的“物理關係”（知識，並非完全一樣），將變體（ $2^n$ ）轉化回因素（ $n$ ）附帶物理關係的形式，從源頭消除熵（假設每個因素只有兩種可能狀態）。這樣所有狀態間的關係可以被確定，要麼肯定發生，要麼絕不發生，也就無需用概率來衡量。因此下面定義的學習目標並非單純降低損失函式，而從確定關係的角度考慮。一個完美訓練好的模型就是兩個狀態空間內所有可能取值間的關係都被確定的模型。

學習目標：是確定（determine）兩個狀態空間內所有可能取值之間的關係，使得熵儘可能最低。

注：對熵不瞭解的朋友可以簡單記住，事件的狀態越確定，熵越小。如絕不發生（概率0）或肯定發生（概率為1）的事件熵小。而50%可能性事件的熵反而大。

為舉例說明，下面就一起考慮用神經網路學習以下兩個集合的不同關聯（OR gate 和 XOR gate）。看看隨著網路結構和關聯的改變，會產生什麼不同情況。尤其是最後網路變深時與淺層神經網路的區別。

注：選擇這種XOR這種簡單關聯的初衷是輸入和輸出空間狀態的個數有限，易於分析變體個數和熵增的關係。

注：用“變體（variation）”是指同一類事物的不同形態，比如10張狗的圖片，雖然外貌各異，但都是狗。

問題描述：集合A有4個狀態，集合B有2個狀態。0和1只是用於表示不同狀態的符號，也可以用0,1,2,3表示。狀態也並不一定表示數字，可以表示任何物理意義。

$A=\{00,01,10,11\}$ $B=\{0,1\}$

方式1：記憶

隨機變數X：可能取值是 $\{00,01,10,11\}$
隨機變數Y：可能取值是 $\{0,1\}$

注：隨機變數（大寫X）是將事件投射到實數的函式。用對應的實數表示事件。而小寫字母x表示對應該實數的事件發生了，是一個具體例項。
網路結構：暫且不規定要學習的關聯是OR還是XOR，先建立一個沒有隱藏層，僅有一個輸入節點，一個輸出節點的神經網路。
表示式： $y=M(x)=\phi(w_{1} \cdot x+b)$ ， $\phi$ 表示sigmoid函式。（只要是非線性即可，relu是目前的主流）
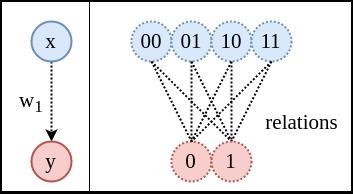
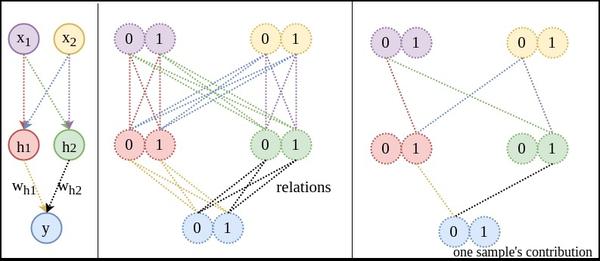
說明：下圖右側中的虛線表示的既不是神經網路的連結，也不是函式中的對映，而是兩個空間中，所有可能值之間的關係（relation）。學習的目的是確定這些狀態的關係。比如當輸入00時，模型要嘗試告訴我們00到1的概率為0，00到0的概率為1，這樣熵 $H(X)=-\sum\limits _ {i} p_{i}(x)logp_{i}(x)$ 才會為零。
關係圖：左側是網路結構，右側是狀態關係圖。輸入和輸出空間之間共有8個關係(非箭頭虛線表示關係)。除非這8個關係對模型來說都是相同的，否則用 $w_{h1}$ 表示 $f:X\rightarrow Y$ 時的熵 $H(M(X),X)$ 就會增加。（ $w_{h1}$ 無法照顧到8個關係，若完美擬合一個關係，其餘的關係就不準確）

注：這裡YJango是 $w_{h1}$ 用表示 $\phi(w_{h1} \cdot x+b)$ 的縮寫。
資料量：極端假設，若用查詢表來表示關係：需要用8個不同的 $(x,y)$ 資料來記住想要擬合的 $f:X\rightarrow Y$ 。

方式2：手工特徵

特徵：空間A的4個狀態是由兩個0或1的狀態共同組成。我們可以觀察出來（計算機並不能），我們利用這種知識 $k()$ 把A中的狀態分解開（disentangle）。分解成兩個獨立的子隨機變數 $H_{1}= \{0,1\}$ 和 $H_{2}= \{0,1\}$ 。也就是用二維向量表示輸入。
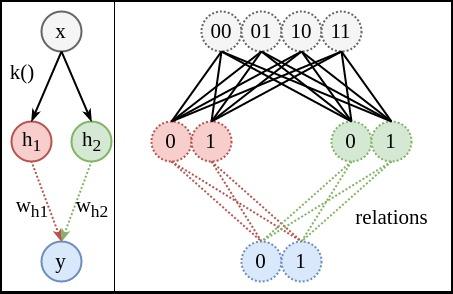
網路結構：由於分成了二維特徵，這次網路結構的輸入需改成兩個節點。下圖中的上半部分是，利用人工知識 $k()$ 將隨機變數 $X$ 無損轉變為 $H_{1}$ 和 $H_{2}$ 的共同表達（representation）。這時 $h_{1}$ 和 $h_{1}$ 一起形成網路輸入。

注：k()旁邊的黑線（實線表示確定關係）並非是真正的神經網路結構，只是方便理解，可以簡單想象成神經網路轉變的。
表示式： $y=M(h)=\phi(W_{h} \cdot h+b)$

注：方便起見， $w_{h1} \cdot h_{1} + w_{h2}\cdot h_{2}$ 寫成了矩陣的表達形式 $W_{h} \cdot h$ ，其中 $b$ 是標量，而 $W_{h}=\left[ \begin{matrix} w_{h1}&w_{h2} \end{matrix} \right]$ ， $\vec{h}=\left[\begin{matrix}h_{1}\\h_{2}\end{matrix}\right]$
關係圖：由於 $k()$ 固定，只考慮下半部分的關係。因為這時用了兩條線 $w_{h1}$ 和 $w_{h2}$ 來共同對應關係。原本需要擬合的8個關係，現在變成了4個（兩個節點平攤）。同樣，除非右圖的4條紅色關係線對 $w_{h1}$ 來說相同，並且4條綠色關係線對 $w_{h2}$ 來說也相同，否則用 $w_{h1}$ 和 $w_{h2}$
表示 $f:X\rightarrow Y$ 時，一定會造成熵 $H(M(X),X)$ 增加。

注：下圖中左側是網路結構圖。右側關係圖中，接觸的圓圈表示同一個節點的不同變體。分開的、並標註為不同顏色的圓圈表示不同節點，左右兩圖連線的顏色相互對應，如紅色的 $w_{h1}$ 需要表示右側的4條紅色關係線。
關聯1：下面和YJango確定想要學習的關聯（函式）。如果想學習的關聯是隻取 $H_{1}$ 或者 $H_{2}$ 的值，那麼該結構可以輕鬆用兩條線 $w_{h1}$ 和 $w_{h2}$ 來表達這4個關係(讓其中一條線的權重為0，另一條為1)。
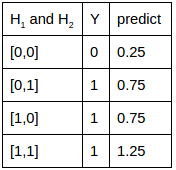
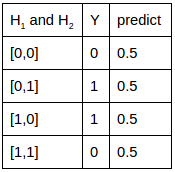
關聯2：如果想學習的關聯是或門，真值表和實際訓練完的預測值對照如下。很接近，但有誤差。不過若要是分類的話，可以找到0.5這個超平面來分割。大於0.5的就是1，小於0.5的就是0，可以完美分開。

注:第一列是輸入，第二列是真實想要學習的輸出，第三列是訓練後的網路預測值。
關聯3：如果想學習的關聯是異或門（XOR），真值表和實際訓練完的預測值對照如下。由於4條關係線無法用單個 $w$ 表達，該網路結構連XOR關聯的分類都無法分開。
資料量：學習這種關聯至少需4個不同的 $([h_{1},h_{2}],y)$ 來擬合 $f_{hy}:H\rightarrow Y$ 。其中每個資料可以用於確定2條關係線。

方式3：加入隱藏層

網路結構1：現在直接把 $h_{1}$ 和 $h_{2}$ 作為輸入（用 $x_{1}$ , $x_2$ 表示），不考慮 $k()$ 。並且在網路結構中加入一個擁有2個節點（node）隱藏層（用 $h_{1}$ 和 $h_{2}$ 表示）。
表示式： $y=M(x)=\phi(W_{h} \cdot \phi(W_{x} \cdot x+b_{x})+b_{h})$
關係圖1：乍一看感覺關係更難確定了。原來還是隻有8條關係線，現在又多了16條。但實際上所需要的資料量絲毫沒有改變。因為以下兩條先驗知識的成立。

注：下圖最右側是表示：當一個樣本進入網路後，能對學習哪些關係線起到作用。
1. 並行： $f_{xh_1}:X_{1},X_{2}\rightarrow H_{1}$ 和 $f_{xh_2}:X_{1},X_{2}\rightarrow H_{2}$ 的學習完全是獨立並行。這就是神經網路的兩條固有先驗知識中的：並行：網路可以同時確定 $f_{xh_1}$ 和 $f_{xh_2}$ 的關聯。也是Bengio大神所指的distributed representation。

注：有效的前提是所要學習的狀態空間的關聯是可以被拆分成並行的因素（factor）。

注： $f_{hy}:H_{1},H_{2}\rightarrow Y$ 就沒有並行一說，因為 $Y$ 是一個節點擁有兩個變體，而不是兩個獨立的因素。但是也可以把 $Y$ 拆開表示為one-hot-vector。這就是為什麼分類時並非用一維向量表示狀態。更驗證了YJango在機器學習中對學習定義：學習是將變體拆成因素附帶關係的過程。
迭代：第二個先驗知識是：在學習 $f_{hy}:H_{1},H_{2}\rightarrow Y$ 的同時， $f_{xh_1}:X_{1},X_{2}\rightarrow H_{1}$ 和 $f_{xh_2}:X_{1},X_{2}\rightarrow H_{2}$ 也可以被學習。這就是神經網路的兩條固有先驗知識中的：迭代：網路可以在確定上一級的同時確定下一級的所有內容。也是Bengio大神所指的compositionality。

注：有效的前提是所要學習的空間的關聯是由上一級迭代形成的。所幸的是，我們所生活的世界幾乎都符合這個前提（有特殊反例）。
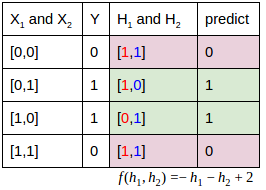
關聯：如果想學習的關聯是異或門（XOR），真值表和實際訓練完的預測值對照如下。

$f_{xh_1}$ 和 $f_{xh_2}$ ：期初若用兩條網路連線表示 $X_{1},X_{2}\rightarrow H_{1},H_{2}$ 的16個關係可能，那麼熵會很高。但用兩條線表示 $X_{1},X_{2}\rightarrow H_{1}$ 的8個關係，模型的熵可以降到很低。下圖中 $f_{xh_1}$ 的輸出值對應紅色數字。 $f_{xh_2}$ 對應輸出值是由藍色數字表達。

$f_{hy}$ :這時再看 $H_{1},H_{2}\rightarrow Y$ 的關係，完全就是線性的。光靠觀察就能得出 $f(h_1,h_2)$ 的一個表達。
資料量：如關係圖1中最右側圖所示，一個輸入[0,0]會被關聯到0。而這個資料可用於學習2+4個關係。也就是說網路變深並不需要更多資料。

模型的熵 $H(M(X),X)$ 與用一條 $\phi(w_{1} \cdot x+b)$ 所要擬合的關係數量有關。也就是說，

變體（variation）越少，擬合難度越低，熵越低。

網路結構2：既然這樣， $X$ 有4個變體，這次把節點增加到4。
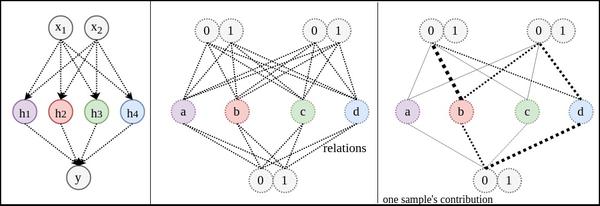
關係圖2：與網路結構1不同，增加到4個節點後，每個節點都可以完全沒有變體，只取一個值。想法很合理，但實際訓練時，模型不按照該方式工作。

注：太多顏色容易眼花。這裡不再用顏色標註不同線之間的對應關係，但對應關係依然存在。
- 問題：因為會出現右圖的情況：只有兩個節點在工作（線的粗細表示權重大小）。 $a$ 和 $c$ 的節點在濫竽充數。這就跟只有兩個節點時沒有太大別。原因是神經網路的權重的初始化是隨機的，資料的輸入順序也是隨機的。這些隨機性使得權重更新的方向無法確定。
討論：網路既然選擇這種方式來更新權重，是否一定程度上說明，用較少的節點就可以表示該關聯？並不是，原因在於日常生活中的關聯，我們無法獲得所有變體的資料。所得資料往往是很小的一部分。較少的節點可以表示這一小部分資料的關聯，但卻無法涵蓋所有變體情況。造成實際應用時效果不理想。
- 緩解：緩解的方式有L2正則化（L2 regularization）：將每層權重矩陣的平方和作為懲罰。
- 表示式： $\lambda/2\cdot\sum\limits_w w^2$ ， $\lambda$ 是懲罰的強弱，可以調節。除以2是為了求導方便（與後邊的平方抵消）。
- 意義：當同一層的權重有個別值過高時，平方和就會增加。而模型在訓練中會降低該懲罰。產生的作用是使所有權重平攤任務，讓 $a,b,c,d$ 都有值。以這樣的方式來使每個節點都工作，從而消除變體，可以緩解過擬合（overfitting）。
- 例如： $L2(W_{hy})=\lambda/2 \cdot (w_{hy1}^2+w_{hy2}^2+ w_{hy3}^2+w_{hy4}^2)$

具有一個隱藏層的神經網路可以模擬任何函式，最糟的情況需要 $k^n$ 個節點。

也叫Universal Approximation Theorem。但最糟的情況是輸入空間有多少個變體，就需要多少個節點。k表示獨立因素的變體個數，n表示獨立因素的個數。上述的例子中最糟的情況需要 $2^2$ 個隱藏節點。而代價也是需要 $k^n$ 個不同資料才可以完美擬合。

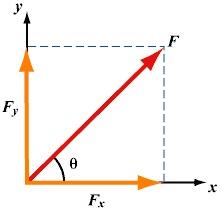
使用條件：淺層神經網路可以分開幾乎所有自然界的關聯。因為神經網路最初就是由於可移動的生物需要預測未來事件所進化而來的。所學習的關聯是過去狀態到未來狀態。如下圖，物理中的力也可以分離成兩個獨立的分力來研究。

但有一種不適用的情況：非函式。

例項：函式的定義是：每個輸入值對應唯一輸出值的對應關係。為什麼這麼定義函式？對應兩個以上的輸出值在數學上完全可以。但是在巨集觀的世界發展中卻不常見。如下圖：
- 時間順流：不管從哪個起點開始，相同的一個狀態（不是維度）可以獨立發展到多個不同狀態（如氧原子可演變成氧分子和臭氧分子）。也就熱力學第二定律的自發性熵增：原始狀態通過物理關係，形成更多變體。
- 時間倒流：巨集觀自然界中難以找到兩個以上的不同狀態共同收回到一個狀態的例子（如氧分子和臭氧分子無法合併成氧原子）。如果這個可以實現，熵就會自發性減少。也就不需要生物來消耗能量減熵。我們的房間會向整齊的狀態發展。但這違背熱力學第二定律。至少在我們的巨集觀世界中，這種現象不常見。所以進化而來的神經網路可以擬合任何函式，但在非函式上就沒有什麼優勢。畢竟生物的預測是從過去狀態到未來狀態。也說明神經網路並不違背無免費午餐定理。
  - 例項：XOR門的輸入空間和輸出空間若互換位置，則神經網路擬合出來的可能性就非常低（並非絕對無法擬合）。

方式4：繼續加深

淺層神經網路可以模擬任何函式，但資料量的代價是無法接受的。深層解決了這個問題。相比淺層神經網路，深層神經網路可以用更少的資料量來學到更好的擬合。上面的例子很特殊。因為 $2\cdot 2=4$ ， $2^2=4$ ，比較不出來。下面YJango就換一個例子，並比較深層神經網路和淺層神經網路的區別。

問題描述：空間 $A$ 有8個可能狀態，空間 $B$ 有2個可能狀態：
$A=\{0,1,2,3,4,5,6,7\}$ $B=\{0,1\}$
網路結構：
- 淺層神經網路：8節點隱藏層
- 深層神經網路：2節點隱藏層 + 3節點隱藏層
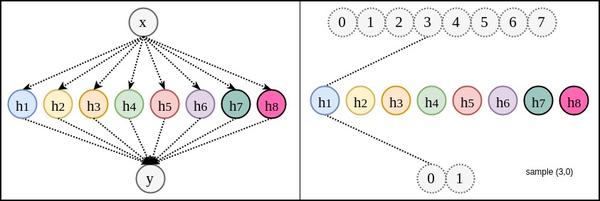
深淺對比：

淺層神經網路：假如說輸入3和輸出0對應。資料 $(3,0)$ 只能用於學習一個節點（如 $h_1$ ）前後的兩條關係線。完美學習該關聯需要所有8個變體。然而當變體數為 $10^{10}$ 時，我們不可能獲得 $10^{10}$ 個不同變體的資料，也失去了學習的意義。畢竟我們是要預測沒見過的資料。所以與其說這是學習，不如說這是強行記憶。好比一個學生做了100冊練習題，做過的題會解，遇到新題仍然不會。他不是學會了做題，而是記住了怎麼特定的題。

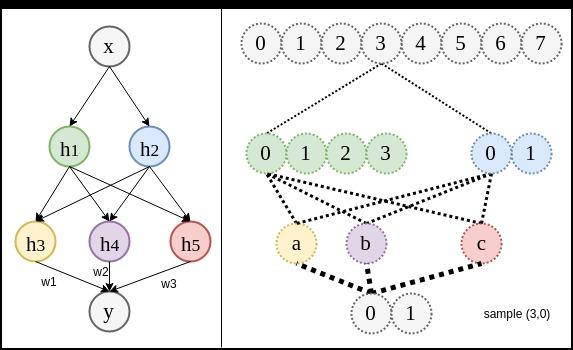
深層神經網路：如果只觀察輸入和輸出，看起來同樣需要8個不同的 $(x,y)$ 訓練資料。但不同 $(x,y)$ 之間有共用部分。比如說，在確定3和0關係時，也同時對所有共用 $w1,w2,w3$ 連線的其他變體進行確定。這樣就使得原本需要8個不同資料才能訓練好的關聯變成只需要3,4不同資料個就可以訓練好。（下圖關係線的粗細並非表示權重絕對值，而是共用度）
深層的前提：使用淺層神經網路好比是用 $y=ax+b$ 解 $a,b$ ，需要2個不同資料。而深層神經網路好比用 $y=ax$ 解 $a$ ，只需要一個數據。無免費午餐定理告訴我們，優化演算法在一個任務上優秀，就一定會在其他任務上有缺陷，深層同樣滿足該定理。如果用 $y=ax$ 去解實際上有 $b$ 的 $y=ax+b$ ，或者去解實際為 $y=ax2+bx+c$ 的關聯時，搜尋效果只會更差。所以深層的前提是： $X$ 空間中的元素可以由 $Y$ 迭代發展而來的。換句話說 $X$ 中的所有變體，都有共用根源 $Y$ （root）。
我們的物理世界：幸運的是，我們的物理世界幾乎都滿足迭代的先驗知識。
- 例項：比如進化。不同動物都是變體，雖然大家現在的狀態各異，但在過去都有共同的祖先。
- 例項：又如細胞分裂。八卦中的8個變體是由四象中4個變體的基礎上發展而來，而四象又是由太極的2個變體演變而來。很難不回想起“無極生太極，太極生兩儀，兩儀生四象，四象生八卦”。（向中國古人致敬，雖然不知道他們的原意）