作者：麥子

轉載請註明：解螺旋·臨床醫生科研成長平臺

上期我們介紹了一個診斷或風險預測模型的評價指標，重新分類指數（Net reclassification index）。主要介紹了一些概念和運用，今天我們就來解決一下技術問題，怎麼算。想來想去，我覺得計算這個東西還是R比較威武。

話說恰好前兩天在知乎上看到某位生物學大大發了這麼一張圖——

啊呀啊喲！不服啊不服哎！可是想來好像又好有道理^(00)^

今天是R語言程式碼的盛（暴）宴（擊），除了NRI的運算，還有蠻多預處理的操作，在哪都能用得著。大家做好戰鬥準備。

R裡有2個包專事計算NRI，分別為nricens和PredictABEL。從最後結果來說，nricens計算出來的是絕對NRI，PredictABEL則為相對NRI。但我們已經知道計算原理了呀，而且它們都能生成新舊模型分類的對照表，所以其實只用其中一個包就都可以計算了。

不過它們還是有一些小小差異，我們就以logistic迴歸模型為例，分別看一下這兩個包，供大家參考選擇。Cox模型引數較多也較複雜，但我相信你看完這篇的講解就能看懂幫助文件中的cox案例，算是留個小作業給你吧~

擬合模型

先用一份示例資料做個模型。這是survival包裡帶有的一份梅奧診所的資料，記錄了418位患者的臨床指標，觀察這些因素與原發性膽汁性肝硬化（PBC）的關係。其中前312位參加了RCT，其他的只參加了觀察佇列。

我們用前312份樣本，做個預測2000天時間點上死亡與否的模型。先載入這份資料看一下。

library(survival)

### logistic迴歸

egData <- pbc[1:312,]

（點選看大圖）

做一個logistic迴歸，我們需要一個結局事件作為因變數，它必需是個分類變數；其次需要若干自變數，它們可以是分類也可以是連續。

這個表中的結局是status，0 = 截尾（刪失），1 = 接受移植，2 = 死亡。研究目的“死亡與否”是個二分類變數，所以要做些變換。

再看time一欄，有的不夠2000天，這些樣本要麼是沒到2000天就死亡了，要麼是刪失了。我們要刪掉2000天內刪失的資料。

egData = egData[egData$time > 2000 |

(egData$time < 2000 & egData$status == 2),]

“[ ]” 表示篩選條件，| 表示“或”，& 為“和”。所以條件句就是egData中的time一列大於2000的保留，或小於2000但同時狀態為死亡的也保留。最後一個“,”別忘了，其在條件句的前面表示對列進行選擇，在其後表示選擇行。

選好後做一個event向量，把status的三個狀態變成死亡 = 1, 未死亡 = 0。

event = ifelse(egData$time < 2000 & egData$status == 2, 1, 0)

ifelse (test, yes, no)大法好啊，前面一個test是邏輯判斷句，其值為真時返回yes的值，為假時返回no的值。所以本句中test就是當time<2000，且status為2（死亡）時，記為1，否則為0。

然後把event合併入原來的表格。

egData = cbind(egData,event)

cbind()是以列合併，另有rbind()以行合併。這樣event就成了最後一列，為結局事件。

然後選擇模型的自變數（predictors）。太多了，選取其中幾個示例。就以年齡、膽紅素、白蛋白為舊模型（standard），三者加上一個凝血酶原時間為新模型（new）。

一般做logistic迴歸是用glm(因變數 ~ 自變數1 + 自變數2 + …… +自變數n,family = binomial('logit'),data = 資料表)，但如果自變數較多的話，前面那個運算式就會很長很長，萬一這些自變數還是基因名或編號，就很想死了。所以順便講一個簡化的辦法，即把那一串先寫成formula。

fml.std <- as.formula(paste('event~',

paste(colnames(egData)[c(5,11,13)],

collapse = '+')))

這裡有好幾層函式，paste() 會把括號中的元素貼上起來，collapse是其中的間隔。colnames() 是獲取表格的列名，[]中的數值向量為所選擇的列序號。這樣如果是一個超大表格，你選中第10~70列還可以寫成“10:70”。

好了，同樣寫出新模型的formula：

fml.new <- as.formula(paste('event~',

paste(colnames(egData)[c(5,11,13,19)],

collapse = '+')))

可以檢視一下，新模型的formula寫成這個效果：

然後像上邊說的那樣用glm()擬合兩個模型。

mstd = glm(fml.std, family = binomial('logit'),

data = egData, x=TRUE)

mnew = glm(fml.new, family = binomial('logit'),

data = egData, x=TRUE)

這樣一長串運算式用剛才命名好的fml.std和fml.new代替就好了。x=TRUE是將來用nricens包計算時要求用到的，表示輸出結果中是否包含所用到的資料表，平時可以不寫。

模型就這樣做完了~ 先不急著計算NRI，先看看它的總體情況。

summary(mstd)

執行這句就得到該模型的描述特徵。

殘差、相關係數、各個自變數的統計顯著性等，注意倒數第二行的AIC，就是上一期提到的赤池資訊準則，表示模型校準度，很少有人彙報呢。

可以用同樣的方法看看新模型。這裡就-不展開了，進入下一環節。

NRI的計算

• 先看nricens包的方法。

library(nricens)

NRI <- nribin(mdl.std = mstd, mdl.new = mnew,

updown = 'category',cut = c(0.3,0.6),

niter = 10000,alpha = 0.05)

填上新舊兩個模型。Cut是判斷風險高低的臨界值，現在我們寫了2個，也就是0~29%為低風險，30%~59%為中風險，60%~100%為高風險。現實中可以查閱相關文獻進行設定，預測風險達到多少需要怎樣干預之類的。

Updown為定義一個樣本的風險是否變動的方式，category是指分類值，即我就熟悉的低、中、高風險，另有一種diff，為連續值。選diff時，cut就設1個值，比如0.02，即認為當預測的風險在新舊模型中相差2%時，即被認為是重新分類了。這種方法用的比較少。

後面幾個引數就比較有意思了，niter為重複取樣的次數，即boostrap方法，不做的話將其設為0就好了；做的話建議至少1000次，這也是預設值，但我（讀書少）見過的研究都10000次。然後將統計顯著性alpha設為0.05。

這樣就可以看到輸出的結果：

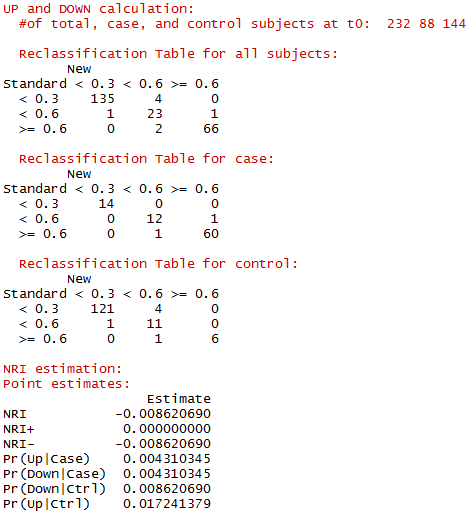
如果不做bootstrap，就是這個結果。有重新分類情況的詳表，最後是NRI和各種變動的概率。第一個NRI如前所述，是絕對NRI，大家可以根據之前的知識和上邊的詳表自己計算驗證一下，此時可手動計算出相對NRI。其他指標隨便看看。

如果做了bootstrap，就會多出一個表：

因為做了10000次重複取樣，相當於有10000個NRI，於是就有了標準誤和置信區間，剛才我們設alpha = 0.05，所以後面的Lower和Upper就是95%置信區間的下界和上界。

同時，做不做bootstrap都會得到一張圖，表示各資料點在新舊模型中的分佈。

預設的Case和Control標籤我覺得不太嚴謹，Case代表結局事件中編號為“1”的組，也就是發生了結局（死亡），Control為“0”，未發生。其實是positive和negative比較貼切吧。反正就這個意思。這張圖也和重新分類表的意思差不多，看看就好。

• 再看PredictABEL包的做法

library(PredictABEL)

pstd <- mstd$fitted.values

pnew <- mnew$fitted.values

先把兩個模型中的預測風險值提出來，也就是模型中的fitted.value。這個包只能從預測風險計算，剛才的nricens包可以用模型，也可以用預測風險（把mdl.std和mdl.new引數換成p.std和p.new）。

reclassification(data = egData,cOutcome = 21,

predrisk1 = pstd,predrisk2 = pnew,

cutoff = c(0,0.30,0.60,1))

cOutcome是結局事件的列序號，剛才我們不是把event放到最後了麼，即第21列，填上。兩個預測風險值也相應填上。這裡的cutoff跟剛才的不一樣，還要填上前面的0和後面的1，成為完整的0~100%的區間。

然後得到一個重新分類表：

跟上邊nricens做的差不多了。不過這個包沒有bootstrap的選項。

接著看下面的結果，這裡的分類NRI是咱們上回說的相加NRI，同樣可以根據上一期的知識手動計算一下。記得咱們並沒有設定bootstrap吧？可這裡也有個95%置信區間，只是內部呼叫了一個更為簡陋的只能計算連續NRI的improveProb()函式做的，而且連續變化的臨界值也不太透明，遂不管了。

最後還有個IDI是指，發生和未發生結局事件樣本的平均預測風險差異，在新模型中提高了0.44%。

延伸、總結和比較

這兩個包當然各有優劣。nricens計算時可控制的引數較多，彙報起來顯得華麗一些。PredictABEL計算結果則多了個IDI和大家喜聞樂見的p值。但也有學者表示，兩個模型的差異未必要求p<0.05。

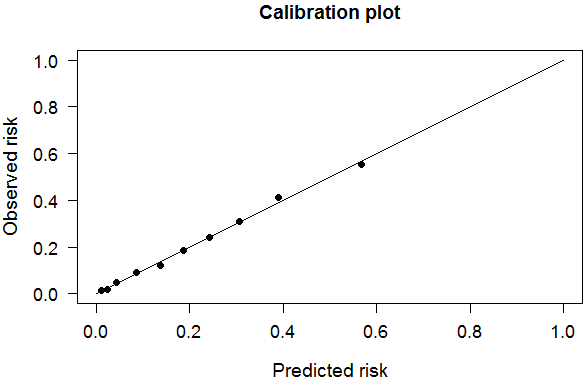
PredictABEL包還有很多有用的功能，比如可以做Hosmer- Lemeshow校準曲線，當然也附送p值（此處沒貼出來）：

區分度箱形圖：

兩個模型的ROC曲線：

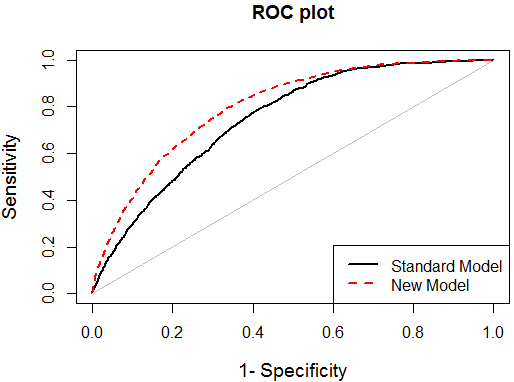
這都是評價一個模型很有價值的參考。