高斯分佈（二）

阿新 • • 發佈：2019-01-04

高斯分佈被廣泛應用於對機器人誤差的建模。在這篇筆記中，我們將會：

介紹如何使用一元高斯分佈、多元高斯分佈和高斯混合模型對機器人誤差進行建模。
介紹求解這些高斯分佈的演算法。
以小球檢測這一實際應用來實踐我們的模型和演算法。

1. 一元高斯分佈

在這一節我們將介紹如何使用一元高斯分佈對機器人誤差進行建模。

在進入正題之前，我們需要首先了解為什麼學習高斯分佈？什麼使得高斯分佈有效並且重要？為什麼使用高斯分佈對噪聲和不確定性進行建模（而不是其他概率分佈模型，比如均勻分佈）？

高斯分佈使得只需要兩個引數就能確定一個連續的概率分佈。這兩個引數分別是均值和方差，這很簡潔。這也使得高斯分佈易於計算和推斷。

高斯分佈有一些較好的數學性質。例如，兩個高斯分佈的積還是高斯分佈。這使得你在對高斯分佈做運算的時候不需要考慮其他的概率分佈。
理論上來說，根據中心極限定理，大量相互獨立的隨機變數，其均值的分佈以高斯分佈為極限。而噪聲和不確定性就是包含大量相互獨立的隨機變數的資料，用高斯分佈對它們進行建模是不二選擇。

說了這麼多，我們來舉個栗子吧，怎樣使用高斯分佈來對一個目標顏色進行建模？

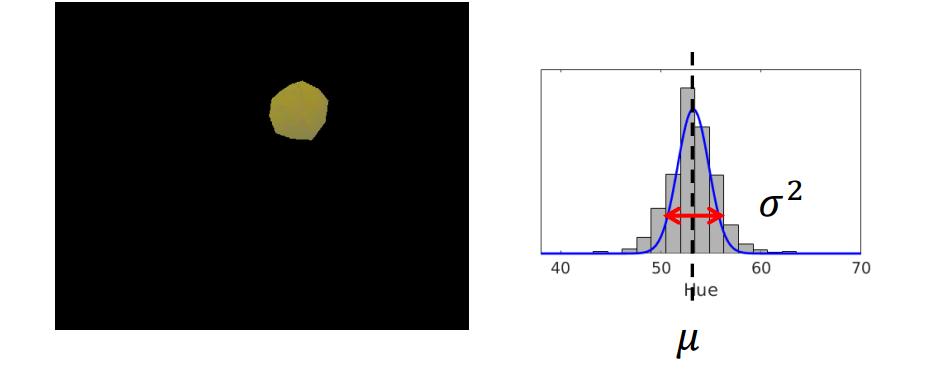
下圖是足球機器人通過頭頂攝像機拍攝到的照片。

顯然，圖片中有兩種顏色的球，黃球和紅球。我們設想這個足球機器人想檢測圖片中的黃球。對於人類來說，一眼就能分辨出黃球在哪，

但對一個機器人來說這並不簡單。機器人讀入的圖片是一個一個畫素的數值，它需要建立從畫素的數值到“黃色”或者“紅色”的對映。

不妨讓我們來看看“黃球”裡面的畫素數值是怎樣的。我們記錄黃球的每個畫素的色相值（Hue，HSV模型中表示色彩的基本屬性，就是平常所說的顏色名稱，如紅色、黃色等），

然後畫出每一個色相值出現次數的柱狀圖如右下。

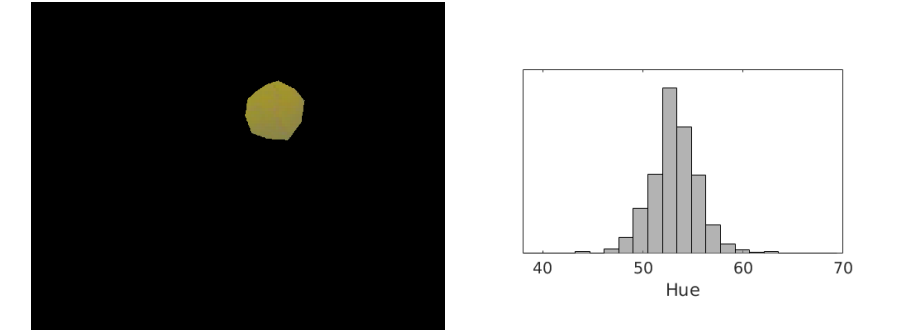
我們可以看到，”黃色“這一種顏色可以有很多個色相值（換成RGB模型也是一樣的），這就是我們所說的噪聲或者不確定性。

從分佈上來看，”黃色“的色相值以大約53為中心然後向兩邊擴散。為了記錄“黃色”，一種方法是記錄每一個“黃色”畫素的色相值，然而這將十分消耗儲存空間，確切來說，有多少畫素就消耗多大的空間。

另一種簡潔有效的方法是使用高斯分佈。

讓我們先來溫故一下高斯分佈的數學表達形式再返回來解釋這個例子吧。

高斯分佈的數學形式如下：

$p(x) = \frac{1}{\sqrt{2\pi} \sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

其中， $x$ 是變數， $p(x)$ 表示 $x$ 的出現的概率， $\mu$ 是均值， $\sigma$ 是標準差（ $\sigma^2$ 是方差）。 $\mu$ 和 $\sigma$ 是之前我們提到的表示一個高斯分佈的兩個引數。

在我們上面的栗子中，假設我們已經完成了對黃色的高斯分佈建模， $x$ 是一個取樣畫素的色相值，那麼 $p(x)$ 就表示該畫素屬於“黃色”的概率。

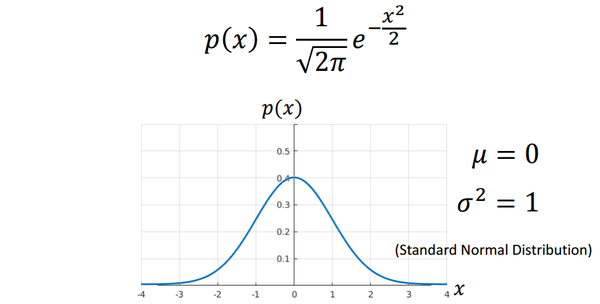
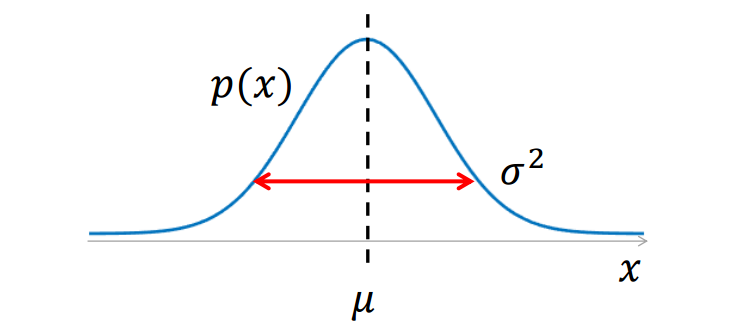
我們繼續介紹高斯分佈，為了更加直觀地瞭解高斯分佈長什麼樣子，我們把高斯分佈畫出來。下圖是 $\mu=0,\sigma=1$ 的情況下的高斯分佈圖（標準高斯分佈）。

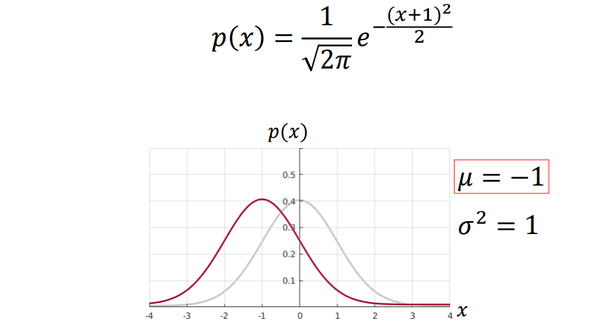
當均值變化而方差不變的時候，可以看作將影象進行了平移。

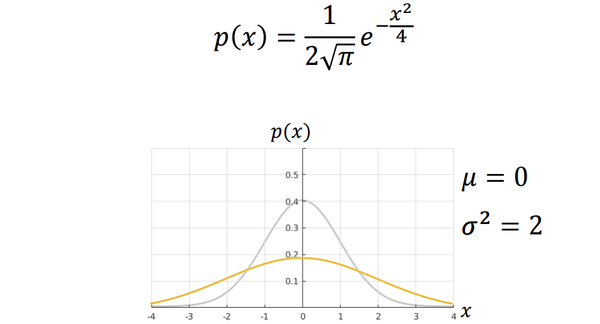
當均值不變，而標準差變化的時候，可以看作將影象進行了“擠”或“壓”（方差越大越扁）。

總結來說， $\mu$ 決定了高斯分佈的對稱軸， $\sigma$ 決定了高斯分佈的擴散程度。

讓我們返回到小球檢測的栗子。我們只使用一個高斯分佈（即兩個值）就可以近似地儲存所有的“黃色”畫素，如下圖。

那麼如何通過資料來求 $\mu$ 和 $\sigma$ 這兩個引數呢？我們將在下一節中介紹最大似然估計方法求解一元高斯分佈。

2. 求解一元高斯分佈：最大似然估計

在這一節，我們將介紹使用最大似然估計（Maximum Likelihood Estimation，MLE）的方法來求解觀測資料的一元高斯分佈。

首先，我們引入似然函式（或者說似然，Likelihood）的概念。

似然指的是在給定模型引數的情況下觀測值出現的概率。它被定義成了一個條件概率 $p(\{x_i\}|\mu,\sigma)$ 。比如，在上一節的小球例子中， $\{x_i\}$ 表示所有“黃色”畫素點的色相值，如果給定了高斯分佈的 $\mu$ 和 $\sigma$ ，我們就能算出 $\{x_i\}$ 出現的概率。

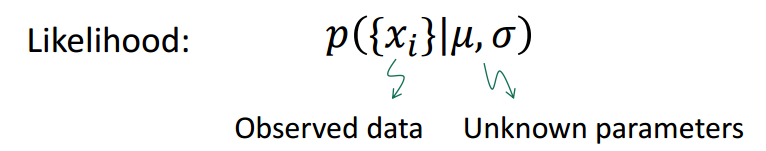
那麼我們的問題就可以表述為，給定觀測值 $\{x_i\}$ ，求 $\mu$ 和 $\sigma$ ，使得似然函式最大：

$\hat{\mu}, \hat{\sigma}=\text{arg}\ \underset{\mu,\sigma}{\max}\ {p(\{x_i\}|\mu,\sigma)}$

其中， $\hat{\mu}$ 和 $\hat{\sigma}$ 表示估計值。

這裡，觀測值 $\{x_i\}$ 是所有的觀測值的集合，我們假設這些觀測值兩兩相互獨立（在我們的小球檢測栗子中也確實是這樣的）。那麼：

$p(\{x_i\}|\mu,\sigma) = \prod_{i=1}^{N}p(x_i|\mu,\sigma)$

這裡， $N$ 表示觀測值集合的大小為 $N$ 。那麼我們的目標就變成了：

$\hat{\mu}, \hat{\sigma}=\text{arg}\ \underset{\mu,\sigma}{\max}\ {\prod_{i=1}^Np(x_i|\mu,\sigma)}$

根據對數函式的單調性( $x_1<x_2\equiv \ln x_1<\ln x_2$ )，取對數再求最大值等價於直接求最大值，即：

$\text{arg}\ \underset{\mu,\sigma}{\max}\ {\prod_{i=1}^Np(x_i|\mu,\sigma)} = \text{arg}\ \underset{\mu,\sigma}{\max}\ln{ \{\prod_{i=1}^Np(x_i|\mu,\sigma)} \}$

那麼我們的目標就變成了：

$\begin{align} \hat{\mu},\hat{\sigma} &=\text{arg}\ \underset{\mu,\sigma}{\max}\ln{ \{\prod_{i=1}^Np(x_i|\mu,\sigma)} \}\\ &=\text{arg}\ \underset{\mu,\sigma}{\max}\sum_{i=1}^{N}\ln p(x_i|\mu,\sigma) \end{align}$

而將 $\ln p(x_i | \mu,\sigma)$ 帶入高斯分佈我們有：

$\begin{align} \ln p(x_i|\mu,\sigma) &= \ln ( \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x_i-\mu)^2}{2\sigma^2}} ) \\ &= -\frac{(x_i-\mu)^2}{2\sigma^2}-\ln\sigma-\ln\sqrt{2\pi} \end{align}$

那麼我們的目標就變成了：

$\begin{align} \hat{\mu},\hat{\sigma} &= \text{arg}\ \underset{\mu,\sigma}{\max}\sum_{i=1}^{N} (-\frac{(x_i-\mu)^2}{2\sigma^2}-\ln\sigma-\ln\sqrt{2\pi}) \\ &= \text{arg}\ \underset{\mu,\sigma}{\max}\sum_{i=1}^{N} (-\frac{(x_i-\mu)^2}{2\sigma^2}-\ln\sigma) \\ &= \text{arg}\ \underset{\mu,\sigma}{\min}\sum_{i=1}^{N} (\frac{(x_i-\mu)^2}{2\sigma^2}+\ln\sigma) \end{align}$

讓我們給後面的目標函式做個記號，令

高斯分佈（二）

2. 求解一元高斯分佈：最大似然估計

高斯分佈（二）

廣義高斯分佈（GGD）

高斯分佈（一）

二維高斯分佈（Two-dimensional Gaussian distribution）的引數分析

正態分佈（Normal distribution）與高斯分佈（Gaussian distribution）

機器學習-多元高斯分佈（異常檢測）

java高級工程師（二）

高斯過程（GP）

面試總結——Java高級工程師（二）

馬爾科夫隨機場（MRF）與吉布斯分佈（Gibbs）

判斷資料是否服從某一分佈（二）——簡單易用fitdistrplus包（轉發）

貝葉斯思想（二）

MySQL MHA高可用方案（二）

全概率公式、貝葉斯公式（二）

機器學習筆記（十）EM演算法及實踐（以混合高斯模型（GMM）為例來次完整的EM）

elixir 高可用系列（二） GenServer

貝葉斯決策論（二）

機器學習(5)——貝葉斯學習（二）

高斯分佈和二項分佈屬於指數分佈族的證明

藍橋杯--2013--高斯日記（模擬）

高斯分佈（二）

2. 求解一元高斯分佈：最大似然估計

相關推薦