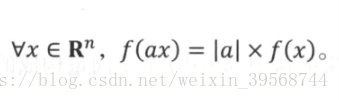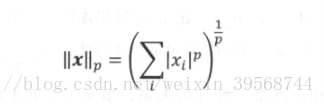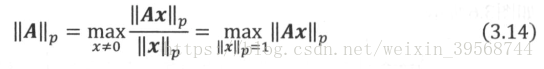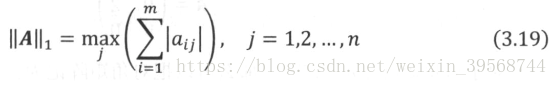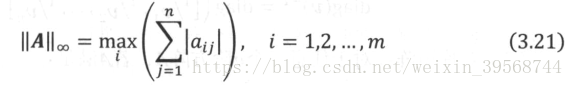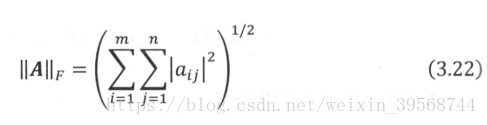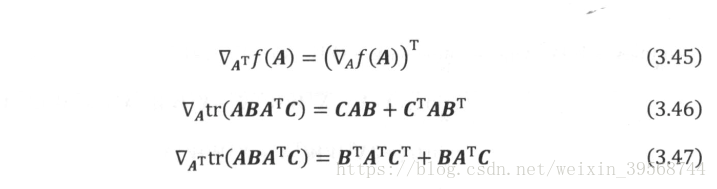深度學習中的線性代數基礎
本文主要總結一些在深度學習領域中比較重要的線性代數基礎,過於基礎的內容沒有進行總結。
一.張量(tensor):在深度學習領域,很多時候資料都是高於二維的,因此,需要一種能夠表示任意維度的資料型別,這就是張量。
二.範數(Norm):範數是數學中的一種基本概念,在泛函分析中,範數是一種定義在賦範線性空間中的函式,滿足相應條件後的函式都可以被稱為範數。下面主要介紹向量範數和矩陣範數並給出常用的幾種範數計算公式。
1.向量範數
在泛函分析中,向量範數是衡量向量大小的一種度量方式。在形式上,向量範數是一個定義域為任意線性空間向量的函式,他把一個向量v對映為一個非負實數值R,即滿足f:v->R
從幾何角度來說,向量x的範數是度量從原點O到點x的距離。從廣義角度來說,對於任意一個函式f:v->R,f只要同時滿足下面3個條件個條件就可以成為範數。
(1)非負性:f(x)>=0,且當f(x)=0時,必有x=0成立。
(2)三角不等式性:f(x+y)<=f(x)+f(y)
(3)齊次性:
在機器學習中,特別是在模型最優化時,範數是正則化的主要手段,用於衡量模型的複雜度,其中最常用到的是p範數,p屬於R,p>=1。p範數的定義為:
0範數:這是一個特殊的p-範數,他表示向量中非0元素的個數。注意,0-範數不是通過上式來定義。事實上我們會發現0範數不是真正的範數,因為他並不滿足前面提到的齊次性性質,也就是f(ax)不等於|a|×f(x),這是因為一個向量乘上一個實數a,若a不等於0,那麼該操作並不會 改變向量中非0元素的個數。
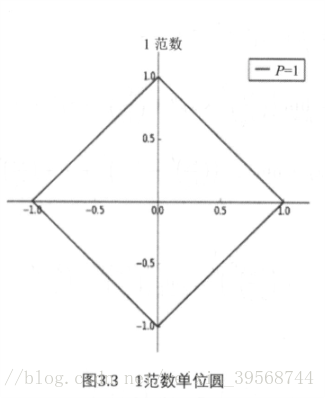
1範數:也被稱為絕對值範數,大小等於向量的每個元素絕對值之和,即:
其中1範數中的單位範數即滿足||x||=1的點{(x1,x2)},如圖3.3所示:
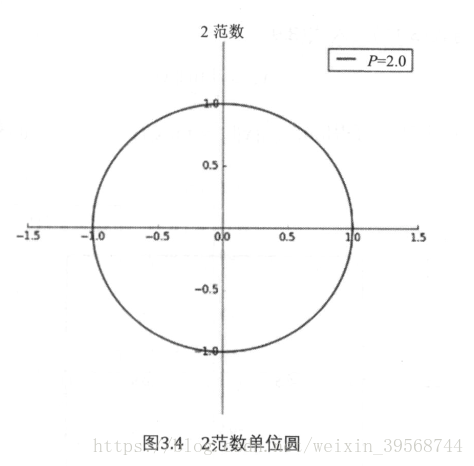
2範數:也被稱為歐幾里得範數,他的大小表示從原點到當前點的歐幾里得距離,即:
2範數也是通常意義上的模,如下圖:
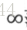

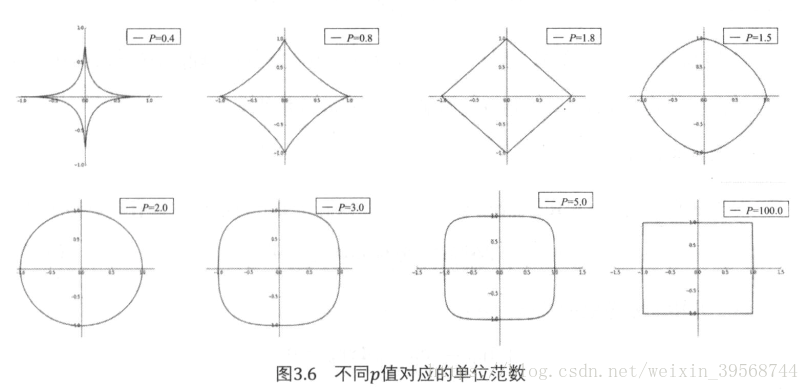
對於一個二維向量x=(x1,x2)^T,他的單位範數隨p值增加的變化過程如下:
2.矩陣範數
上面討論了常用的向量範數,範數的概念同樣可以推廣到矩陣領域,由此產生了矩陣範數的概念:對於任意一個函式f:A->R,函式f只要同時滿足下面4個條件就可以稱為矩陣範數:
(1)非負性:f(A)>=0,且當f(A)=0時,必要A=0成立
(2)齊次性:任取A屬於R(m×n),f(aA)=|a|×f(A)
(3)三角不等式性:f(A+B)<=f(A)+f(B)
(4)矩陣乘法的相容性:對於任意兩個可乘的矩陣A屬於R(m×k)和矩陣B屬於R(k×n),滿足f(AB)<=f(A)×f(B)
為了與向量範數對應,用來表示矩陣的p範數,矩陣範數同樣有多種不同的形式,但最常用的是與向量範數緊密相連的誘導範數,首先給出誘導範數的概念。
定義1:設是向量x的範數,
是矩陣A的範數,如果對於任意的矩陣A與向量x滿足:
成立則稱矩陣範數與向量範數
是相容的。
定義2:設是向量p範數,定義:
則是一個矩陣範數,並且稱該矩陣範數是由向量範數
所誘導的誘導範數。
由向量p範數,可以誘匯出常用的矩陣p範數。
1範數:記為,是由向量1範數誘導的矩陣,矩陣1範數的定義為:
矩陣1範數也稱為列和範數。
2範數:記為,是由向量2範數誘導的矩陣範數,矩陣2範數的定義為:
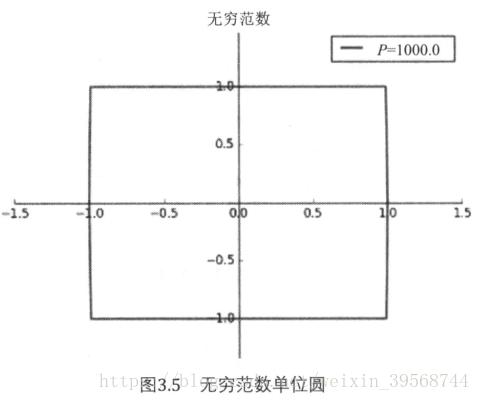
無窮範數:記為,是由向量無窮範數誘導的矩陣範數,矩陣無窮範數的定義為:
矩陣無窮範數也被稱為行和範數。
此外,在深度學習中,還經常用到另外一個矩陣範數,稱為Frobenious範數,簡稱F範數,其定義為:
特殊的矩陣與向量:(1)對角矩陣(2)對稱矩陣(3)單位向量(4)正交向量(5)正交矩陣
特徵值分解:分而治之是演算法設計的一種常用策略,通過把一個物體分解為不同的子部分,有時可以更好地理解整體特性。
奇異值分解:
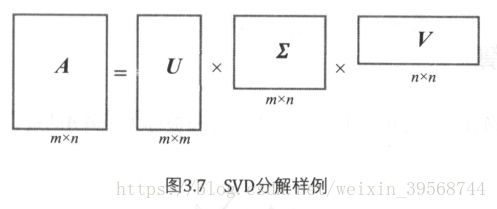
奇異值分解(Singular Value Decompositon,簡稱SVD),是線性代數中另一種非常重要的矩陣分解演算法,特徵值分解只適用於n階方陣,並且不是所有的n階方陣都存在特徵分解,而SVD的應用更廣,它適用於任意給定的m×n階實數矩陣A。除了適用於將維,SVD還能應用於很多機器學習的工程領域,下圖展示了SVD的分解樣例:
形式化來說,設矩陣,則矩陣A可以分解為下面的形式:
在很多情況下,不需要使分解的結果準確還原矩陣A,只需要接近於A即可。事實上,奇異值與特徵值的性質相似,在中間的對角矩陣中也是從大到小排列,而且奇異值的值減少特別快,在很多情況下,前百分之10甚至百分之1的奇異值的和就已經佔了全部的奇異值之和的百分之99以上了。也就是說,可以用前r大的奇異值來近似描述矩陣,因此可以將式子化簡為約等於。
跡運算: