from: http://blog.sciencenet.cn/blog-1255140-1025724.html

函數擬合

現實中各種各樣的問題都可以歸結為函數問題。比如醫生診斷疾病，他得到病人檢查的各種參數，體溫、血壓、血檢報告和CT掃描的各種數據等，然後判斷他是否健康，還是得了什麽病。這個例子裏，各種參數就是函數的自變量，病人的健康情況是函數值，比如健康是0，有病是1，也可以更具體，肝病是1，胃病是2等。又比如識別物體，輸入的是物體的像素數據，輸出的是物體的類別，是貓是狗，還是蘋果梨子等。

機器學習是從樣例中總結出規律，本質上是函數擬合。從有限的樣本中得到一個函數，使它能擬合樣本數據，然後把它應用到新的樣例中。我們學習知識的過程也類似。比如我們每次見了狗，都跟小孩子說這是一條狗，經歷過幾次後，小孩子就能總結出規律，知道狗是什麽樣子，以後出現未見過的狗，他也會判斷。

神經元模型

人工神經網絡的研究受到了真實神經網絡的啟發。神經元是人工神經網絡的基本要素，它表示為：

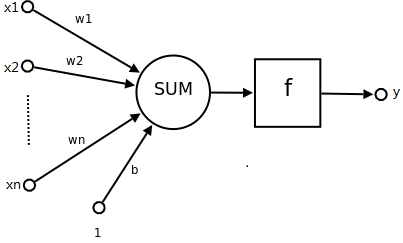
Sum是求和函數，x1、x2……xn是輸入，w1、w2、……wn是權重：

Sum（x1，x2，……，xn）= w1x1 + w2x2 +……+ wnxn + b

f是激活函數。最簡單的激活函數是符號函數，如下：

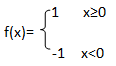
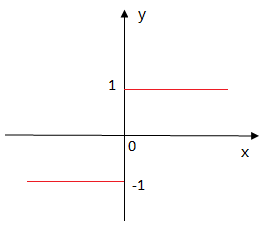
所以這個神經元模型表示的函數是：y=f (x1，x2，……，xn)

=f (w1x1 + w2x2 +……+ wnxn + b)

線性劃分

上面的神經元模型雖然簡單，但它可以實現很多函數。比如可用它來表示大部分布爾函數。用1和-1分別表示真和假。設置w1=w2=0.5，b=-0.8，這時神經元是邏輯AND函數。將b改為-0.3，則變成OR函數。但它無法表示XOR函數（當x1≠x2時，輸出為1，否則為0）。

由於這個神經元函數是線性函數，所以可以把它看作是n維空間的超平面決策器。對於超平面一側的樣例，神經元輸出1，另一側則輸出-1。

當空間的點是線性可分時，可用單個神經元劃分，否則不行。比如下面的左圖，紅色的點和藍色的點可用一根直線分開，這些點可用神經元分類，而右邊是XOR函數，無法用直線分開，解決：多層神經剛落。

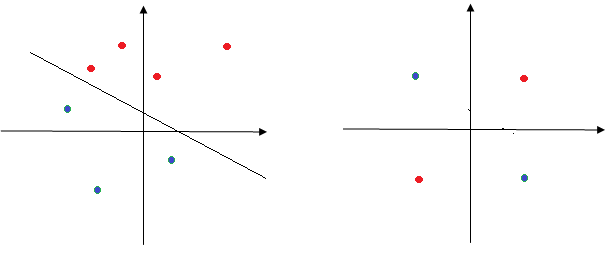
多層網絡

單層網絡的功能太弱，引入多層網絡，除了輸入層和輸出層外，其他的層是隱藏層。

前饋神經網絡是最基本的多層網絡，上一層的神經元和下一層的每個神經元都有連接，不能跨層連接，同一層的也不連接。可以看出這實質上是個復合函數。

除了前饋神經網絡外，還有其他類型的網絡，它們不遵守上面的這些限定。

前饋神經網絡

學習算法

教小孩子什麽是蘋果，先告訴他這幾個是蘋果，他自己會總結出一些特征。當出現一個梨子時，他若判斷為蘋果，就告訴他這是錯的。他會根據這個梨子和蘋果的差異，修改他關於蘋果的認知，這樣反復幾次後，就會掌握蘋果這個概念。

學習算法是神經網絡中最核心的要素，神經網絡的學習和上面小孩子的學習有些相似。學習的目的是獲得網絡連接的正確權值。有各種各樣的學習算法，反向傳播算法是很重要的一種。它將網絡輸出和正確的函數值進行比較，根據兩者的差異修改權值，再將修改後得到的網絡輸出和正確值比較，再根據差異修改，這樣多次重復，逐漸縮小兩者的差異。

下面是反向傳播算法的圖示，圖中的f(x)是激活函數。

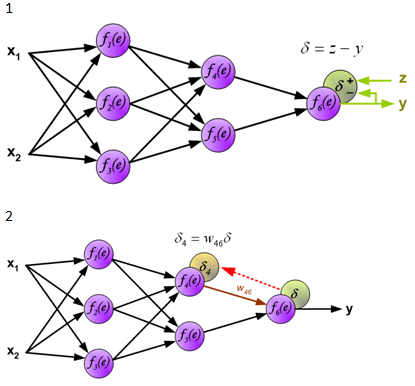
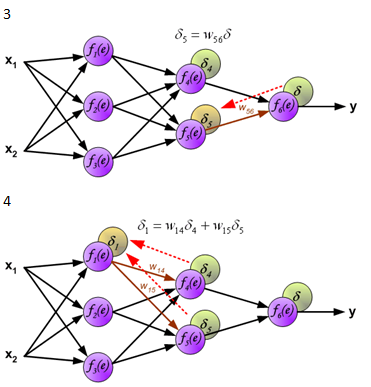
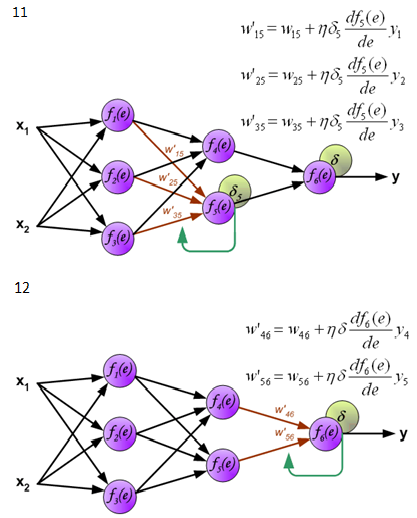
圖片來源：http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

關於函數擬合，線性，非線性的一些見解（轉）