數構與演算法 | 什麼是大 O 表示演算法時間複雜度
正文:
開篇我們先思考這麼一個問題:一臺老式的 CPU 的計算機執行 O(n) 的程式,和一臺速度提高的新式 CPU 的計算機運 O(n2) 的程式。誰的程執行效率高呢?
答案是前者優於後者。為什麼呢?我們從時間複雜度分析就可以知道。
1、什麼是時間複雜度?
在進行演算法分析時,語句總的執行次數 T(n) 是關於問題的規模n 的函式,進而分析 T(n) 隨 n 的變化情況並確定 T(n) 的數量級,演算法的時間複雜度,也就是演算法的時間度量,記作:T(n) = O(f( ))。它表示隨問題的規模 n 的增大,演算法的執行時間的增長率 f(n) 的增長率相同,稱作演算法的漸近時間複雜度,簡稱為時間的複雜度,其中 f(n) 是問題規模n的某個函式。
這樣用大寫 [ O( ) ] 來體現演算法時間複雜度的記法,我們就稱之為大O記法。例如:O(n)、O(1)、O(n2)、O(log n) 等等。一般情況下,隨著 n 的增大,T(n) 增長最慢的演算法為最優演算法。
2、推導大O階的方法
如何推導大O階的表示方法,總結了三句口訣:
- 用時間1取代運算時間中的所有加法常數。
- 在修改後的執行的函式中,只保留最高階項。
- 如果最高階項存在且不是1,則去除與這個項相乘的常數。得到的結果就是大O階。
說了太多文字顯得太抽象,我們來看看一個例子你就明白了。
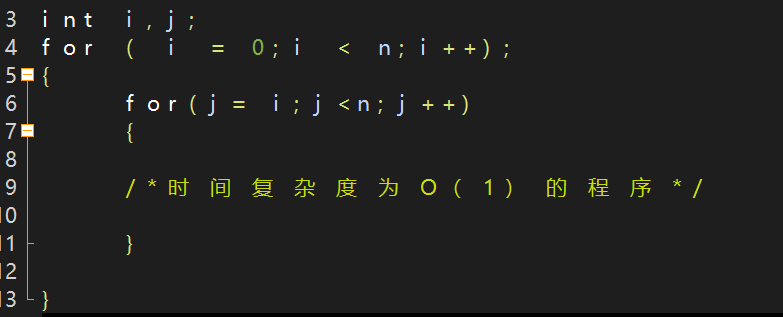
如圖這個時間複雜度你知道是多少嗎?
分析:
當 i = 0時,內迴圈執行了 n 次,
當 i = 1時,內迴圈執行了 n-1 次,
····
當 i = n-1時。執行了 1 次,所以總的執行次數為:n = (n-1)+(n-2)+ ··· + 1= n(n+1)/2 = n2/2+n/2。
由上面的公式可得:第一條程式碼中沒有加法常數項,不考慮;第二條只保留最高階項,因此保留 n2/2;第三條去除這個項相乘的常數,所以去除了 1/2;最終我們得到的程式碼段時間複雜度就是 O(n2)。
所以有了上面這個公式我們就可以對一般的時間複雜度大O的推導求解,其實理解大 O 推導不算難,難得是對數列的一些相關運算。更多的是考察你的數學功底。所以能不能寫出好的高效率程式碼和你的數學功底有關哦。數學真的很重要(認真臉)。
3、一些常用的O( )時間複雜度推導
例1:O(1)常數階
int sum = 0, n = 100; /* 執行一次 */
sum = (1+n) *n/2; /* 執行一次 */
printf("the sum is:%d",sum); /* 執行一次 */
我們可以看出執行次數的函式是 f(n) = 3。根據我們上面的大O階公式 1 可以得到,把常數項 3 改為 1,在保留最高階時發現沒有最高階項,所以時間複雜度為大 O(1)。也就是說,無論演算法是 3 次還是 30 次,哪怕是 300 次,這些只要是常數項,它的時間複雜度都為大 O(1),而不是O(3)、O(30)、O(300)。即我們稱之為常數階。
例2:O(n)線性階
從上面的這段程式碼我們可以看出,它的時間複雜度為O(n),因為迴圈體中的程式碼需要執行n次。
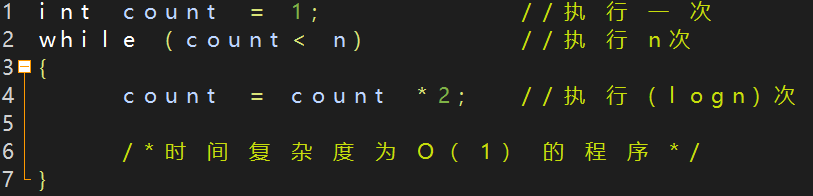
例3:O(log n)對數階
上面程式碼我們可以看出,count = count * 2 之後就距離 n 更近里布,也就是說,有多少個 2 相乘後大於 n,就退出迴圈。所以我們可以由 2x = n 推匯出 x = log2n ,像這樣的迴圈時間複雜度,我們就稱為對數階的複雜度即為 O(log n)。
例4:O(n2)平方階
這是有 2 個 for 語句組成的迴圈,是每一個迴圈程式碼執行 n次,所以整個程式碼就是 n*n 次,所以時間複雜度為 O(n2) 。
注意:如果外面的的迴圈次數不是 n 而是 m 那麼時間複雜度就變為了 O(m*n) ,所以,迴圈的時間複雜度就等於迴圈體的的複雜度乘上該迴圈的執行次數。
資料結構中我們一般常用的時間複雜度表示有:O(1)、O(n)、O(n2)、O(log n)、O(nlog n)、O(n3)、O(2n)。
按時間複雜度所耗費的時間從大到小排序依次為:
O(1) < O(log n) < O(n) < O(nlog n) < O(n2) < O(n3) < O(2n)
到這裡,我們就可以清楚的明白了開篇的問題,為什麼老式 CPU 程式執行速率比新式的 CPU 執行效率高的原因就是應為O(n)< O(n2) 時間複雜度的關係,所以能寫出好的演算法是可以讓計算機變得輕鬆的。
4、時間複雜度的三種情況
1.最好情況時間複雜度:
顧名思義,看名字你就知道,就是程式碼執行的次數為一次即為最好的 O(1)。這是要我們寫程式碼最想要的。但是這是不現實的。
2.最壞情況時間複雜度:
同樣的看名字你也可以知道,這是程式碼執行的總次數很多,每次都要執行 n 次,所以表示為 O(n)。這是我們寫程式碼最不想要的。當然這也是不現實的。
3.平均時間複雜度:
就是把最好情況時間複雜度和最壞情況時間複雜度求取一平均值,這是我們寫程式碼最有意義的,因為這是期望的執行時間,所以在寫程式碼時應當考慮這一點。
5、演算法空間複雜度
所謂演算法的空間複雜度就是通過計算機演算法所需求的存在空間實現。計算公式可以表示為:S(n) = O( f(n) ),其中,n為問題的規模,f(n) 為語句關於 n 所佔儲存空間的函式。
一般情況下,一個程式在機器上執行時,除了考慮到程式的本身執行指令,常數,變數和輸入資料外,還需要考慮儲存對資料操作的儲存單元。
我們在寫程式碼時完全可以用空間換取時間,兩者不存在絕對的好與壞,這麼用好二者關係取決於你用在什麼地方。所以,實際情況還是要根據工程程式碼做最完美的選擇。
6、總結
- 時間複雜度大O表示方法的由來。
- 大O推導的表示方法和常用的大O表示法時間複雜度。
- 時間複雜度的三種情況:最好情況、最壞情況和平均情況。
- 演算法空間複雜度,適當情況可以用空間換取時間。
=====================(完)===================