Ramble Over The Cloud~
正交矩陣、正規矩陣和酉矩陣
在數學中,正規矩陣 是與自己的共軛轉置交換的復係數方塊矩陣,也就是說, 滿足
其中 是 的共軛轉置。
如果 是實係數矩陣,那麼條件簡化為 其中 是 的轉置矩陣。
矩陣的正規性是檢驗矩陣是否可對角化的一個簡便方法:任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣的矩陣都是正規矩陣。
在復係數矩陣中,所有的酉矩陣、埃爾米特矩陣和斜埃爾米特矩陣都是正規的。同理,在實係數矩陣中,所有的正交矩陣、對稱矩陣和斜對稱矩陣都是正規的。兩個正規矩陣的乘積也不一定是正規矩陣
酉矩陣
n階複方陣U的n個列向量是U空間的一個標準正交基,則U是酉矩陣(Unitary Matrix)。
一個簡單的充分必要判別準則是:
方陣U的共扼轉置乘以U等於單位陣,則U是酉矩陣。即酉矩陣的逆矩陣與其伴隨矩陣相等。
酉方陣在量子力學中有著重要的應用。酉等價是標準正交基到標準正交基的特殊基變換。
其中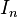 為n階單位矩陣,
為n階單位矩陣, 為U的共軛轉置,則稱其為么正矩陣或酉矩陣。即,矩陣U為么正矩陣,當且僅當其共軛轉置
為U的共軛轉置,則稱其為么正矩陣或酉矩陣。即,矩陣U為么正矩陣,當且僅當其共軛轉置 為其逆矩陣:
為其逆矩陣:
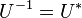 。
。
若么正矩陣的元素都是實數,其即為正交矩陣。與正交陣G不會改變兩個實向量的內積類似,
么正矩陣U不改變兩個復向量的內積:
在數學中,正規矩陣
 是與自己的共軛轉置交換的復係數方塊矩陣,也就是說,
是與自己的共軛轉置交換的復係數方塊矩陣,也就是說, 滿足
滿足
其中 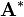 是
是
 的共軛轉置
的共軛轉置
如果 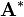 是實係數矩陣,那麼條件簡化為
是實係數矩陣,那麼條件簡化為
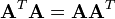 其中
其中
 是
是
 的轉置矩陣。
的轉置矩陣。
矩陣的正規性是檢驗矩陣是否可對角化的一個簡便方法:任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣的矩陣都是正規矩陣。
在復係數矩陣中,所有的酉矩陣、埃爾米特矩陣和斜埃爾米特矩陣都是正規的。同理,在實係數矩陣中,所有的正交矩陣、對稱矩陣和斜對稱矩陣都是正規的。兩個正規矩陣的乘積也不一定是正規矩陣
酉矩陣
n階複方陣U的n個列向量是U空間的一個標準正交基,則U是酉矩陣(Unitary Matrix)。
一個簡單的充分必要判別準則是:
方陣U的共扼轉置乘以U等於單位陣,則U是酉矩陣。即酉矩陣的逆矩陣與其伴隨矩陣相等。
酉方陣在量子力學中有著重要的應用。酉等價是標準正交基到標準正交基的特殊基變換。
|
其中
若酉矩陣的元素都是實數,其即為正交矩陣。與正交矩陣G不會改變兩個實向量的內積類似, 么正矩陣U不改變兩個復向量的內積: 若 酉矩陣的特徵值都是絕對值為1的複數,即分佈在複平面的單位圓上,因此酉矩陣行列式的值也為1。 其中V是酉矩陣,Σ是主對角線上元素絕對值為1的對角陣。 對任意 n,所有n階酉矩陣的集合關於矩陣乘法構成一個群。 性質
|


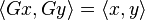

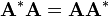
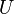 為n階方陣,則下列條件等價:
為n階方陣,則下列條件等價: