筆者在前面的兩篇文章中介紹了圖的兩種實現方法：

接下來筆者將介紹圖遍歷演算法，與樹的遍歷類似，圖的遍歷也需要訪問所有頂點一次且僅一次；此外，圖遍歷同時還需要訪問所有的弧一次且僅一次。

圖的遍歷概述

圖的遍歷都可理解為，將非線性結構轉化為半線性結構的過程。經遍歷而確定的弧型別中，最重要的一類即所謂的樹邊，它們與所有頂點共同構成了原圖的一棵支撐樹（森林），稱作遍歷樹（traversal tree）本文要介紹的BFS將是其中的一種。以遍歷樹為背景，其餘各種型別的邊，也能提供關於原圖的重要資訊，比如其中所含的環路等。

圖中頂點之間可能存在多條通路，故為避免對頂點的重複訪問，在遍歷的過程中，通常還要動態地設定各頂點不同的狀態，並隨著遍歷的程序不斷地轉換狀態，直至最後的“訪問完畢”。圖的遍歷更加強調對處於特定狀態頂點的甄別與查詢，故也稱作圖搜尋（graph search）。

與樹遍歷一樣，作為圖演算法基石的圖搜尋，本身也必須能夠高效地實現，如深度優先、廣度優先、最佳優先等基本而典型的圖搜尋，都可以線上性時間內完成。若頂點數和邊數分別為 n 和 e，則這些演算法自身僅需 0 (n + e）時間。

圖的廣度優先搜尋概述

各種圖搜尋之間的區別，體現為邊分類結果的不同，以及所得遍歷樹（森林）的結構差異。其決定因素在於，搜尋過程中的每一步迭代，將依照何種策略來選取下一接受訪問的頂點。

通常，都是選取某個已訪問到的頂點的鄰居。同一頂點所有鄰居之間的優先順序，在多數遍歷中不必講究。因此，實質的差異應體現在，當有多個頂點已被訪問到，應該優先從誰的鄰居中選取下一頂點。比如，廣度優先搜尋（breadth-first search, BFS）採用的策略，可概括為：越早被訪問到的頂點，其鄰居越優先被選用

於是，始自圖中頂點s的BFS搜尋，將首先訪問頂點s；再依次訪問s所有尚未訪問到的鄰居；再按後者被訪問的先後次序，逐個訪問它們的鄰居；…；如此不斷。由於每一步迭代都有一個頂點被訪問，故至多迭代 O (n）步。另一方面，因為不會遺漏每個剛被訪問頂點的任何鄰居，故對於無向圖必能覆蓋 s 所屬的連通分量（connected component），對於有向圖必能覆蓋以 s 為起點的可達分量（reachable component）。倘若還有來自其它連通分量或可達分量的頂點，則再從該頂點出發，重複上述過程。

圖的廣度優先搜尋的程式碼實現

首先來看看再遍歷演算法中節點和弧使用到的屬性：
節點：

    private int status = 0;  //狀態 0 undiscovered "未發現"  1 discovered "已發現"   2 visited "已完成"
    private int parent = -1;

弧：

    private int type;  
    //弧型別：0 CROSS 跨邊  1 TREE（支撐樹）

遍歷程式碼

    //廣度優先，並生成bfs樹
  public void bfsTree(int index) {
      this.reload();//復位所有節點和弧的狀態
      int v = index;
      do {
          if(allNodes[v].getStatus() == 0) {
              this.bfs(v);
          }
      }while(index !=(v = (++v%size)));
  }

  public void bfs(int v) {
      Queue<Integer> list = new LinkedList<Integer>();
      list.add(v);
      allNodes[v].setStatus(1);

      while(!list.isEmpty()) {
          v = list.poll();
          //列舉v的所有鄰居 u
          for(int u=0; u<size; u++) {
              if(getEdge(v, u)!=null) {
                  //如果節點i尚未被發現
                  if(allNodes[u].getStatus() == 0) {
                      //發現該節點
                      allNodes[u].setStatus(1);
                      //並設定支撐樹(index為i的parent)
                      nodeGraphs[v][u].setType(1);
                      allNodes[u].setParent(v);
                      list.add(u);
                  }else {
                   //如果節點i已被發現，則將邊index->i 歸為跨邊
                   nodeGraphs[v][u].setType(0);
                  }
              }
          }
          //至此，v節點訪問完畢
          allNodes[v].setStatus(2);
      }
  }

  //獲取與節點node的相連結的弧，不存在返回false
  public Edge getEdge(int start, int end) {
    return nodeGraphs[start][end];
  }

演算法的實質功能，由子演算法 bfs（）完成。對該函式的反覆呼叫，即可遍歷所有連通或可達域。仿照樹的層次遍歷，這裡也藉助佇列 list，來儲存已被發現，但尚未訪問完畢的頂點。因此，任何頂點在進入該佇列的同時，都被隨即標為”已發現”狀態。

bfs（）的每一步迭代，都先從 list 中取出當前的首頂點 v；再逐一核對其各鄰居 u 的狀態並做相應處理；最後將頂點 v 置為 “訪問完畢” 狀態，即可進入下一步迭代。

若頂點 u 尚處於”未發現”狀態，則令其轉為”已發現” 狀態，並隨即加入佇列 list。實際上，每次發現一個這樣的頂點 u，都意味著遍歷樹可從 v 到 u 拓展一條邊。於是，將邊（v, u）標記為樹邊（tree edge），並按照遍歷樹中的承襲關係，將 v 記作 u 的父節點。

若頂點 u 已處於 “已發現” 狀態（無向圖），或者甚至處於“已完成“ 狀態（有向圖），則意味著邊（v, u）不屬於遍歷樹，於是將該邊歸類為跨邊（cross edge)

bfs（）遍歷結束後，所有訪問過的頂點通過 parent指標依次聯接，從整體上給出了原圖某一連通或可達域的一棵遍歷樹，稱作廣度優先搜尋樹，或簡稱 BFS 樹（BFS tree）。

例項給出了一個

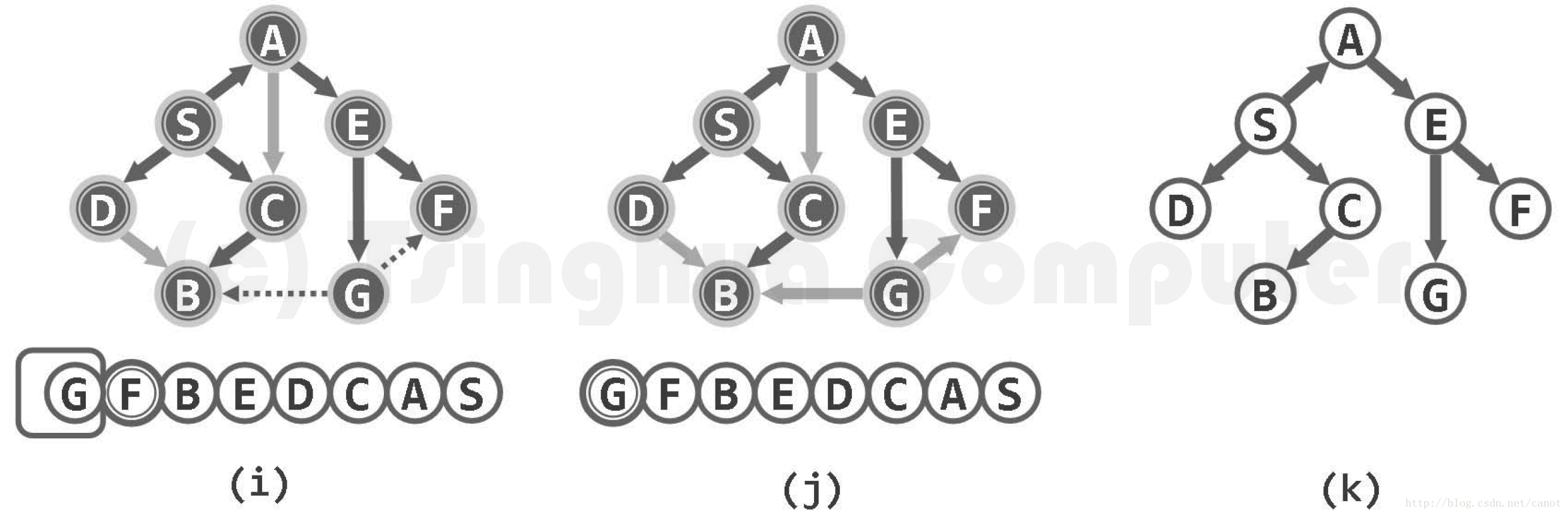
下圖展示了一個含8個頂點和11條邊的有向圖，起始於頂點S的BFS搜尋過程。注意觀察輔助佇列（下方）的演變，頂點狀態的變化，邊的分類與結果，以及BFS樹的生長過程

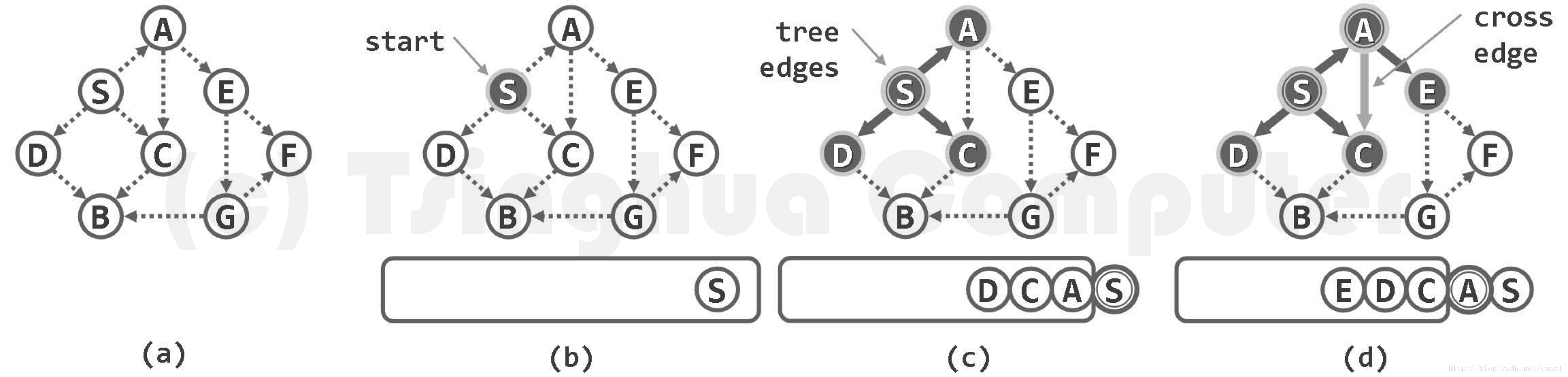
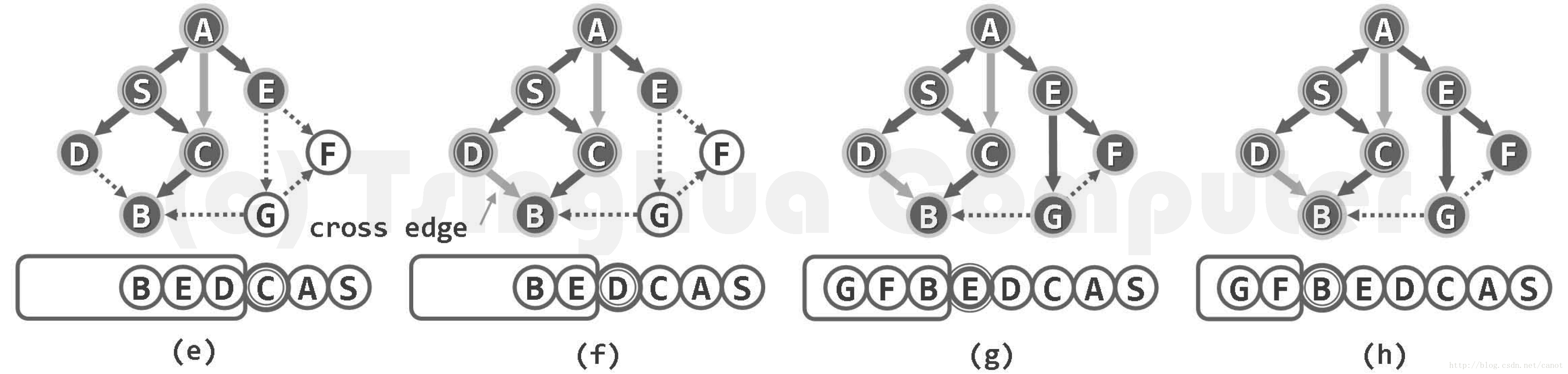
不難看出，bfs (s）將覆蓋起始項點 s 所屬的連通分量或可達分量，但無法抵達此外的頂點。而上層主函式 bfsTree（）的作用，正在於處理多個連通分量或可達分量並存的情況。具體地，在逐個檢查頂點的過程中，只要發現某一頂點尚未被發現，則意味著其所屬的連通分量或可達分量尚未觸及，故可從該頂點出發再次啟動 bfs (），以遍歷其所屬的連通分量或可達分量。如此，各次 bfs（）周用所得的 BFS 樹構成一個森林，稱作 BFS 森林。

複雜度

除作為輸入的圖本身外，BFS 搜尋所使用的空間，主要消耗在用於維護頂點訪問次序的輔助佇列、用於記錄頂點和邊狀態的標識位向量，累計 O (n) + O (n) + O (e) = O (n + e）。

時間方面，首先需花費 0 (n + e）時間復位所有頂點和邊的狀態。不計對子函式 bfs（）的呼叫，bfsTree（）本身對所有項點的列舉共需 0 (n）時間。而在對 bfs（）的所有呼叫中，每個頂點、每條邊均只耗費 0 (1）時間，累計 O (n + e）。綜合起來，BFS 搜尋總體僅需 0 (n + e）時間。