完全二叉樹是由滿二叉樹而引出來的。對於深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。

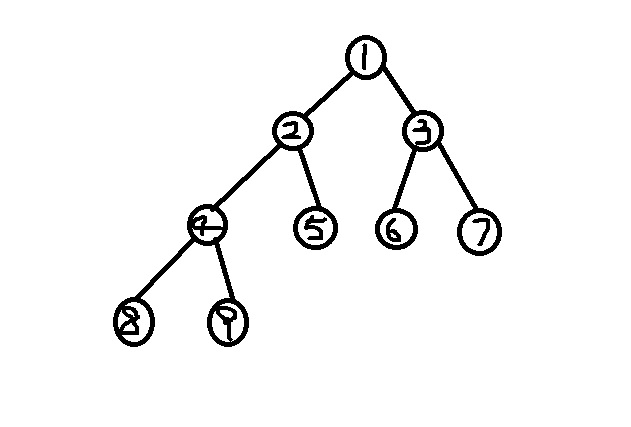
比如下面這棵樹就是一棵完全二叉樹

通過圖片我們可以瞭解到它的建立過程是從上到下，從左至右的，也就是說，它是一層一層建立的。

完全二叉樹有以下基本性質：

1. 對於一棵有n個結點的完全二叉樹，其任意結點 i (1<=i<=n)，如果 i = 1, 則結點 i 是二叉樹的根，無雙親; 如果 i>1,則其雙親parent(i)是結點 i/2.

2. 如果 2i>n; 則結點 i 無左孩子（結點 i 為葉子結點 ）; 否則其左孩子lchild(i)是結點 2i.

3. 如果 2i+1>n, 則結點 i 無右孩子; 否則其右孩子rchild(i)是結點 2i+1.

   建立一棵完全二叉樹，關鍵要處理好親子之間的關係，對此我做出瞭如下總結：

一種是邊生孩子邊找關係，在生成新結點時把它的父親結點指出來； 還有一種就是 生完孩子在找關係，即先生成樹中的所有結點，再去指出結點之間的父子關係.

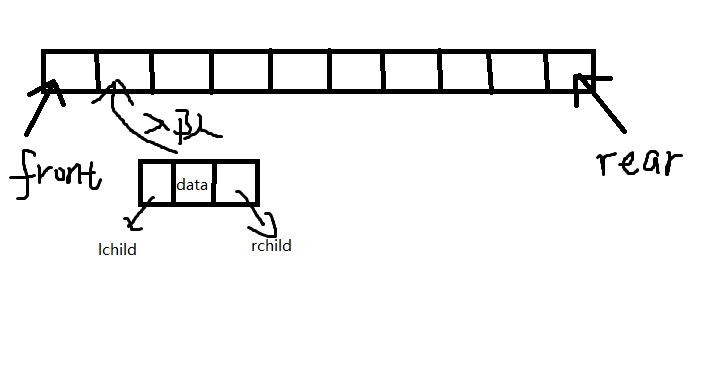
為了確定樹之間的這種關係，我們需要藉助一個輔助的儲存空間，比如一個數組或是堆疊或佇列，這裡我用一個順序佇列來實現.

採用先生孩子後找關係的順序來生成這顆二叉樹，先生成樹中所有結點並將其入隊，再指出其父子關係，圖片描述如下：

具體實現程式碼如下：

#include<stdio.h>
 

#include<stdlib.h>

typedef struct bitree
{
  int data;
  struct bitree *lchild,*rchild;
}BiTNode;

//////////////函式宣告 
BiTNode* CreateBiTree(int *,int);
void PreOderTraverse(BiTNode *);
void DestoryBiTree(BiTNode *);

int main()
{
    BiTNode *t;

    int a[10] = {1,4,6,7,2,5,3,9,8};                 //樹中結點的資料 
 


    t = CreateBiTree(a,10);

    PreOderTraverse(t);

    DestoryBiTree(t);

    return 0;
}

///////////////////建立二叉樹
BiTNode* CreateBiTree(int *a,int n)
{
    BiTNode *root,*p;                   
    BiTNode *bitQueue[n];                        //定義一個佇列用來存放完全二叉樹
    int front=1,rear=1;                          //初始化佇列

////////////////////////////////////////////////生成結點併入隊 
    for(int i=0; i<n; i++)
    {
      if(*(a+i) == 0)
         p = NULL;
      else
      {
        p = (BiTNode *)malloc(sizeof(BiTNode));
        p->data = *(a+i);
        p->lchild = p->rchild = NULL;
      } 
        bitQueue[rear++] = p;                    //p結點入隊,隊尾指標加 1
        if(i==0) root = p;                       //初始化根節點
    }
/////////////////////////////////////////////找出結點間的父子關係 
    while(front != rear)                         //如果佇列不為空                               
    {
        p = bitQueue[front];                    //當前要找關係的結點 
        if(p != NULL)
        {
            if(2*front <= n)    p->lchild = bitQueue[2*front];            
            //根據完全二叉樹性質，如果2i<n,(n為該二叉樹中總結點個數),則該結點有左孩子為2i
            if(2*front+1 <= n)  p->rchild = bitQueue[2*front+1];
            //如果2i<n,(n為該二叉樹中總結點個數),則該結點有左孩子為2i+1
        }
        front++;                               //隊頭指標加 1，指向下一個結點
    }

   return root;
}

//////////////////前序遍歷
void PreOderTraverse(BiTNode *t)
{
 if(t)                   //如果樹不為空
 {
   printf("%d ",t->data);
   PreOderTraverse(t->lchild);
   PreOderTraverse(t->rchild);
 }
}

//////////////////銷燬二叉樹
void DestoryBiTree(BiTNode *t)
{
  if(t)
  {
      if(t->lchild)
          DestoryBiTree(t->lchild);
      if(t->rchild)
          DestoryBiTree(t->rchild);
      free(t);
      t = NULL;
  }
}