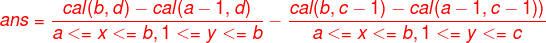2301: [HAOI2011]Problem b

Time Limit: 50 Sec  Memory Limit: 256 MB
Submit: 7732  Solved: 3750
[Submit][Status][Discuss]

Description

對於給出的n個詢問，每次求有多少個數對(x,y)，滿足a≤x≤b，c≤y≤d，且gcd(x,y) = k，gcd(x,y)函式為x和y的最大公約數。

100%的資料滿足：1≤n≤50000，1≤a≤b≤50000，1≤c≤d≤50000，1≤k≤50000

Input

第一行一個整數n，接下來n行每行五個整數，分別表示a、b、c、d、k

Output

共n行，每行一個整數表示滿足要求的數對(x,y)的個數

Sample Input

2

2 5 1 5 1

1 5 1 5 2


 

Sample Output

14

3

題解：簡化為計算a/k<=x<=b/k,c/k<=y<=d/k滿足gcd(x,y)=1的x,y有多少對；cal(n,m)代表1<=x<=n,1<=y<=m滿足gcd(x,y)=1的(x,y)對數，則根據容斥定理:

#include<iostream>
#include<stdio.h>
#define ll long long
using namespace std;
const ll N=50007;
ll prime[N],mu[N];
bool mark[N];
void getmu()
{
        mu[1]=1;
        int cnt=0;
        for(int i=2;i<=N;i++){
                if(!mark[i])
                        prime[cnt++]=i,mu[i]=-1;
                for(int j=0;j<cnt&&i*prime[j]<=N;j++){
                        mark[i*prime[j]]=1;
                        if(i%prime[j]){
                                mu[i*prime[j]]=-mu[i];
                        }else{
                                mu[i*prime[j]]=0;break;
                        }
                }
                mu[i]+=mu[i-1];//後面不會再用到mu[i],所以可以直接記為字首和
        }
}
ll cal(ll n,ll m){
        if(n>m)
                swap(n,m);
        ll ans=0;
        for(ll l=1,r;l<=n;l=r+1){
                r=min(n/(n/l),m/(m/l));
                ans+=(mu[r]-mu[l-1])*(n/l)*(m/l);
        }
        return ans;
}
int main()
{
        int T;
        ll a,b,c,d,k;
        getmu();
        scanf("%d",&T);
        while(T--){
                scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
                a=(a-1)/k,b=b/k,c=(c-1)/k,d=d/k;
                printf("%lld\n",cal(b,d)-cal(a,d)-(cal(c,b)-cal(c,a)));
        }
        return 0;
}