比特幣錢包，金鑰，地址

錢包就是金鑰所在之處，錢包是私鑰的容器，通過有序檔案或者簡單的資料庫實現或者用原有的私鑰通過單向雜湊函式生成每一個新的私鑰，並將新的金鑰順序連線。

比特幣錢包包含的是私鑰而不是比特幣，一個使用者可以有一個或者多個私鑰的錢包，錢包中含有成對的私鑰和公鑰，使用者用私鑰來簽名交易，比特幣是以交易輸出的形式來儲存在區塊鏈中。（避免地址重複原則—每個比特幣地址只能用一次交易）

數字金鑰由使用者生成並且儲存在一個簡單的資料庫中。

錢包分為確定性錢包和非確定性錢包。
非確定性錢包是隨機生成的私鑰的集合，Just a Bunch Of Key(JBOK),一次性生成足夠數量的私鑰，儲存所有的副本，每一把都需要備份，一旦丟失則錢包控制的資金就丟失了，不鼓勵使用。

確定性錢包也叫種子錢包（HD錢包屬於確定性錢包），從一個主金鑰生成海量的子金鑰，一旦控制了主金鑰，就可以生成所有的子金鑰，確定性錢包是樹狀結構，僅備份一次就行。確定性錢包的好處：1.安全（可以離線儲存主金鑰）2.許可權控制（樹形結構對應各分支部門）3.便於記賬

金鑰（去中心化信任和控制，所有權認證，密碼學證明）
公鑰：銀行賬號
私鑰：PIN碼或者支票簽名（儲存在錢包檔案內）
私鑰可以生成特定訊息的簽名，不洩露私鑰的同時對公鑰驗證
並非所有的比特幣地址都是公鑰，還有可能是指令碼（其他支付物件）

金鑰用途：生成簽名、證明所有權、創造比特幣靚號地址和紙錢包

私鑰（k）經過單向橢圓曲線相乘演算法變為公鑰（K）

公鑰（K）經過單向雙雜湊函式變為比特幣地址

單向不可逆數學函式：素數冪和橢圓曲線乘法
生成私鑰相當於生成1—2^256之間的一個隨機數
（偽隨機數生成器CSPRNG）
程式設計角度：密碼學安全的隨機源中取一長串隨機位元組，然後進行SHA256雜湊
演算法運算，產生一個256位的數字然後驗證（著重理解SHA256演算法）


通過橢圓曲線乘法（比特幣程式大多用OpenSSL加密庫計算或者呼叫EC_POINT_mul（））從私鑰得到公鑰（不可逆轉），K=k*G（G為生成點的常數點）


橢圓曲線：
無窮遠點相當於0在加法中，可表示為X=Y=0
+相當於實數相加
EXP：
P3=P1+P2
P3可以在P1和P2之間畫一條線來確定，直接與橢圓曲線上的一點相交，該點即為
P3’=（x，y），P3=（x，-y）。
若P1和P2為同一點，P1 P2的連線就是P1的切線，曲線上有且只有一個新的點與
該切線相交
若P1和P2有相同的X的值，不同Y的值，切線完全垂直，P3為無窮遠點
若P1就是無窮遠點，那麼P3=P2，P2亦然

EXP：
給定橢圓上點P，如果K為整數，則KP=P+P+P+P……P（K次）   加法的拓展，不停的加

比特幣地址=RIPEMD160（SHA256（K））（通常是經過Base58Check）

Base58Check編碼：比特幣地址字首為0x00，私鑰編碼字首為0x80，checksum=sha256(sha256(prefix+data))取前4個位元組

最終比特幣地址為：prefix+data+checksum前4位元組

橢圓加密演算法ECC（加密/解密  簽名  生成軟體序列號）

無窮遠點與平常點

射影平面座標系A（X:Y:Z）

橢圓曲線（維爾斯塔拉斯方程）  y^2*z+a1*x*y*z+a3*y*z^2=x^3+a2*x^2*z+a4*x*z^2+a6*z^3  橢圓曲線不是橢圓

橢圓曲線的切線斜率  k=(3*x^2+2*a2*x+a4+a1*y)/(2*y+a1*x+a3)

由連續到離散：滿足有限域Fp上的三個法則

加密解密基於一個數學上的難題（RSA）：給定兩個素數p、q很容易相乘得到n，而對n進行

因式分解相對困難

首先，A選定一個橢圓曲線Ep（a，b）選取其中一點G

A選擇一個私鑰k，並且生成公鑰K=kG

A將K,G,Ep（a，b）傳給B

B將明文編碼到Ep（a，b）上的一點M，並且產生一個隨機數r（r<n）

B計算點C1=M+rK，C2=rG，將C1 C2傳給A

A收到資訊後可以計算出M，並將M解碼得到明文

加密/解密引數選擇：T=（p,a,b,G,n,h）p,a,b用來確定一條橢圓曲線，G為基點，n為點

G的階，h是橢圓曲線上所有點的個數m與n相除的整數部分

滿足條件：p越大越安全，但是計算速度會變慢，200位左右可以滿足一般的安全要求

p!=n*h

pt!=1(mod n)   1<=t<=20

4*a^3+27*b^2!=0(mod p)

n位素數

h<=4

 安全雜湊演算法SHA256

輸入報文最大長度要求為2^64bit，然後按512bit一組進行分組，最終產生的是一個256bit的報文摘要

首先，附加填充位元，對輸入的報文進行填充使報文長度與448模512同餘（長度=448mod512）填充位元範圍是1到512，填充位元最高位為1，其餘位為0（後面會加上一個64bit原始報文的長度資訊）

然後，附加長度值，將64bit表示的初始報文的位長度附加在填充的報文後

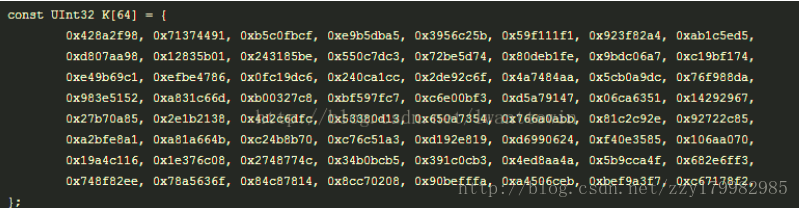
初始化快取，用一個256bit的快取來存放雜湊函式的中間及最終結果，每一步使用一個32bit的常數值KT和一個32bit的WT

 

A=0x6A09E667

B=0xBB67AE85

C=0x3C6EF372

D=0xA54FF53A

E=0x510E527F

F=0x9B05688C

G=0x1F83D9AB

H=0x5BE0CD19

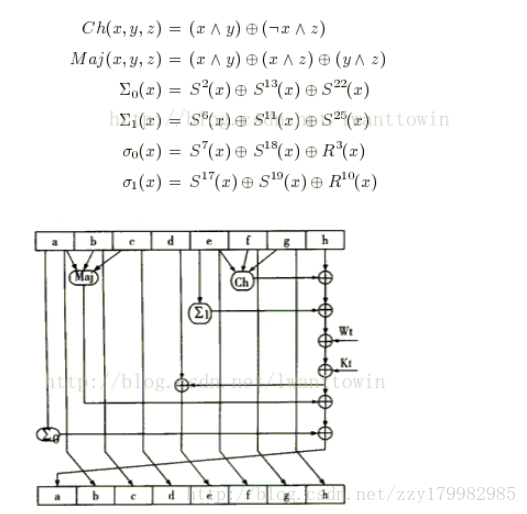
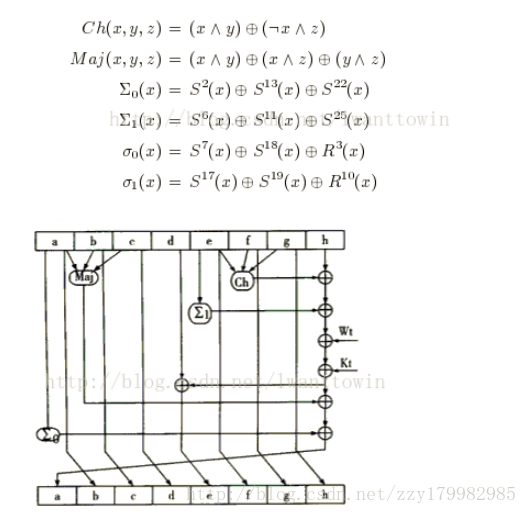
用六種基本邏輯函式處理報文分組序列，64步迭代運算

 

參與運算的都是32bit的數，WT是分組之後的報文，512bit=32bit*16.也就是說WT

T=1,2,3,4……16由該組報文產生

WT T=17,18,19……64由WT推導公式計算出來，WT的遞推公式為：

WT=σ1（Wt-2）+Wt-7+σ0（Wt-15）+Wt-16

不斷處理分組的報文，SHA256演算法最後一個分組產生的輸出就是報文摘要

SHA-1與MD5的比較

　　因為二者均由MD4匯出，SHA-1和MD5彼此很相似。相應的，他們的強度和其他特性也是相似，但還有以下幾點不同：

　　對強行供給的安全性：最顯著和最重要的區別是SHA-1摘要比MD5摘要長32 位。使用強行技術，產生任何一個報文使其摘要等於給定報摘要的難度對MD5是2^128數量級的操作，而對SHA-1則是2^160數量級的操作。這樣，SHA-1對強行攻擊有更大的強度。

　　對密碼分析的安全性：由於MD5的設計，易受密碼分析的攻擊，SHA-1顯得不易受這樣的攻擊。

　　速度：在相同的硬體上，SHA-1的執行速度比MD5慢。

RIPEMD160演算法：是針對MD4和MD5演算法缺陷分析提出的演算法，摘要長度160，用BouncyCastle實現

將摘要轉換為40位16進位制的數