FFT演算法講解——麻麻我終於會FFT了!
阿新 • • 發佈:2019-01-05
FFT——快速傅立葉變換
這塊不寫東西空蕩蕩的,我決定還是把FFT的定義給貼上吧
FFT(Fast Fourier Transformation)是離散傅氏變換(DFT)的快速演算法。即為快速傅氏變換。它是根據離散傅氏變換的奇、偶、虛、實等特性,對離散傅立葉變換的演算法進行改進獲得的。
這三段話其實一點用也沒有
FFT是幹什麼的
FFT在演算法競賽中就有一個用途:加速多項式乘法(暴言)
簡單來說,形如 的代數表示式叫做多項式,可以記作,其中叫做多項式的係數,是一個不定元(就是不可以合併),不表示任何值,不定元在多項式中最大項的次數稱作多項式的次數
如果我們當前有兩個多項式,現在要把他們乘起來(求卷積),最樸素的做法就是
這樣的複雜度是的,十分不美觀,FFT就是要將這個過程優化為
前置技能
多項式
見上文
複數
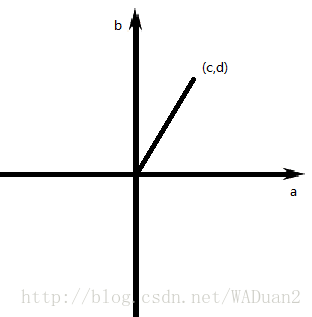
複數形如,其中
叫作複數的實部,叫做複數的虛部
複數相乘的值,即也是一個複數,同時我們也得到了複數的乘法法則
複數可以用這種方式表示出來
複數乘法的在複平面中表現為輻角相加,模長相乘
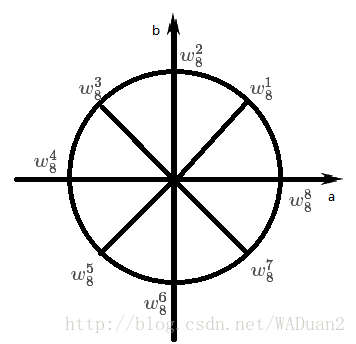
單位根
複數滿足稱作是次單位根,下圖包含了所有的次單位根(圖中圓的半徑是1)
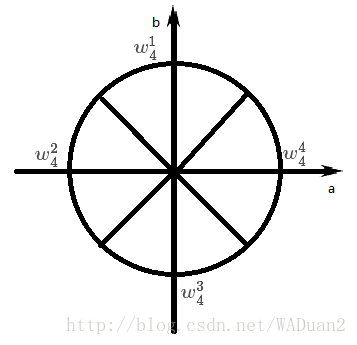
同樣的,下圖是所有的4次單位根
聰明的你也許已經發現了單位根的些許性質,即
這兩個要記住,一會很有用
多項式的係數表達法
我們有多項式,令,則稱為多項式的係數表示法
在係數表示法下,計算多項式乘法是的
多項式的點值表達法
任取個互不相同的,對分別求值得到,那麼稱為多項式在下的點值表示法
可以把多項式想象成一個次函式,點值表示法就是取下每一個橫座標時對應的點,因為次函式可以由個點確定下來(可以將每一個點列一個次方程),所以維點值與維繫數一一對應
更重要的一點,點值表示法下的乘法運算獲得了簡化
兩個多項式,分別取點和,就會取到點;
令,因為,所以